【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
参考答案:
【答案】(1)![]() ;(2)该公可若想获得10000万元的年利润,此设备的销售单价应是50万元.
;(2)该公可若想获得10000万元的年利润,此设备的销售单价应是50万元.
【解析】(1)根据点的坐标,利用待定系数法即可求出年销售量y与销售单价x的函数关系式;
(2)设此设备的销售单价为x万元/台,则每台设备的利润为(x﹣30)万元,销售数量为(﹣10x+1000)台,根据总利润=单台利润×销售数量,即可得出关于x的一元二次方程,解之取其小于70的值即可得出结论.
(1)设年销售量y与销售单价x的函数关系式为y=kx+b(k≠0),将(40,600)、(45,550)代入y=kx+b,得:
![]() ,
,
解得:![]() ,
,
∴年销售量y与销售单价x的函数关系式为y=﹣10x+1000.
(2)设此设备的销售单价为x万元/台,则每台设备的利润为(x﹣30)万元,销售数量为(﹣10x+1000)台,根据题意得:
(x﹣30)(﹣10x+1000)=10000,
整理,得:x2﹣130x+4000=0,
解得:x1=50,x2=80.
∵此设备的销售单价不得高于70万元,∴x=50.
答:该设备的销售单价应是50万元/台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
我们知道,
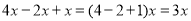 ,类似地,我们把
,类似地,我们把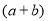 看成一个整体,则
看成一个整体,则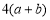
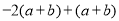 =
= .“整体思想”是初中数学解题中的一种重要的思想方法,它在多项式的化简与求职中应用极为广泛.
.“整体思想”是初中数学解题中的一种重要的思想方法,它在多项式的化简与求职中应用极为广泛.尝试应用:
(1)把
 看成一个整体,合并
看成一个整体,合并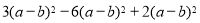 的结果为_______.
的结果为_______.(2)已知
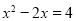 ,求
,求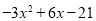 的值.
的值.拓广探索:
(3)已知
 ,求
,求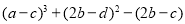 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.

请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.
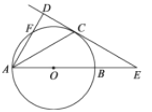
(1)求证:AD⊥CD;
(2)若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14,
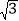 ≈1.73,结果保留一位小数.)
≈1.73,结果保留一位小数.) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,平行四边形ABCD的坐标分别为A(﹣1,0)、B(0,2)、C(4,2)、D(3,0),点P是AD边上的一个动点,若点A关于BP的对称点为A',则A'C的最小值为( )
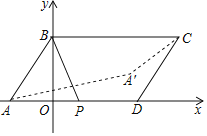
A.
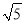 B.
B.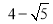 C.
C.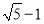 D.1
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E,F分别是AB,AD的中点,若△AEF的面积为5cm2,则平行四边形ABCD的面积是_____cm2.
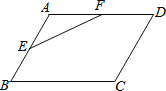
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某月的月历,用如图恰好能完全遮盖住月历表中的五个数字,设带阴影的“
 ”形中的5个数字的最小数为a.
”形中的5个数字的最小数为a. 请用含a的代数式表示这5个数;
请用含a的代数式表示这5个数; 这五个数的和与“
这五个数的和与“ ”形中心的数有什么关系?
”形中心的数有什么关系? 盖住的5个数字的和能为105吗?为什么?
盖住的5个数字的和能为105吗?为什么?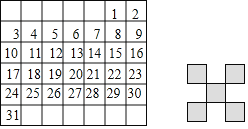
相关试题

