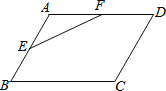
【题目】如图,在平行四边形ABCD中,E,F分别是AB,AD的中点,若△AEF的面积为5cm2,则平行四边形ABCD的面积是_____cm2.
参考答案:
【答案】40
【解析】
连结BD,根据三角形中位线定理得出EF∥BD,EF=![]() BD,那么△AEF∽△ABD,利用相似三角形面积比等于相似比的平方求出S△ABD=4S△AEF=20cm2,根据平行四边形的性质得出AD∥BC,AD=BC,由等底等高的三角形面积相等得出S△CBD=S△ADB=20cm2,于是SABCD=40cm2.
BD,那么△AEF∽△ABD,利用相似三角形面积比等于相似比的平方求出S△ABD=4S△AEF=20cm2,根据平行四边形的性质得出AD∥BC,AD=BC,由等底等高的三角形面积相等得出S△CBD=S△ADB=20cm2,于是SABCD=40cm2.
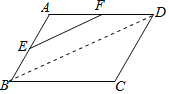
解:如图,连结BD.
∵E、F分别是AB、AD的中点,
∴EF∥BD,EF=![]() BD,
BD,
∴△AEF∽△ABD,
∴![]() ,
,
∴S△ABD=4S△AEF=20cm2,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴S△CBD=S△ADB=20cm2,
∴SABCD=40cm2,
故答案为:40.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.
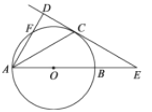
(1)求证:AD⊥CD;
(2)若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14,
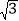 ≈1.73,结果保留一位小数.)
≈1.73,结果保留一位小数.) -
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价
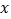 (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.(1)求年销售量
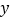 与销售单价
与销售单价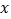 的函数关系式;
的函数关系式;(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
-
科目: 来源: 题型:
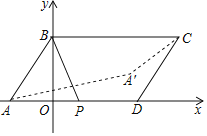
查看答案和解析>>【题目】如图,在平面直角坐标系中,平行四边形ABCD的坐标分别为A(﹣1,0)、B(0,2)、C(4,2)、D(3,0),点P是AD边上的一个动点,若点A关于BP的对称点为A',则A'C的最小值为( )
A.
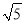 B.
B.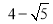 C.
C.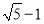 D.1
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某月的月历,用如图恰好能完全遮盖住月历表中的五个数字,设带阴影的“
 ”形中的5个数字的最小数为a.
”形中的5个数字的最小数为a. 请用含a的代数式表示这5个数;
请用含a的代数式表示这5个数; 这五个数的和与“
这五个数的和与“ ”形中心的数有什么关系?
”形中心的数有什么关系? 盖住的5个数字的和能为105吗?为什么?
盖住的5个数字的和能为105吗?为什么?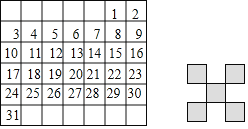
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5cm,BC=2cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D即停止,当运动时间为_____秒时,△MBN为等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】再读教材:
宽与长的比是
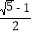 (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.
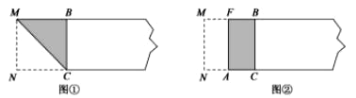
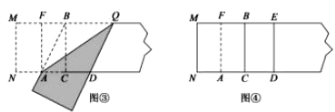
第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,
问题解决:
(1)图③中AB=________(保留根号);
(2)如图③,判断四边形 BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
相关试题

