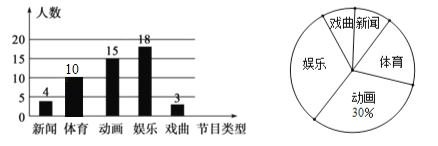
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.

请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
参考答案:
【答案】(1)50人;(2)补图见解析;(3)540人;(4)![]()
【解析】(1)根据动画类人数及其百分比求得总人数;
(2)总人数减去其他类型人数可得体育类人数,据此补全图形即可;
(2)用样本估计总体的思想解决问题;
(3)根据题意先画出树状图,得出所有情况数,再根据概率公式即可得出答案.
(1)这次被调查的学生人数为15÷30%=50人;
(2)喜爱“体育”的人数为50﹣(4+15+18+3)=10人,补全图形如下:
(3)估计全校学生中喜欢娱乐节目的有1500×![]() =540人;
=540人;
(4)列表如下:
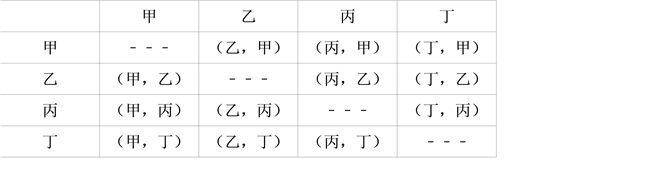
所有等可能的结果为12种,恰好选中甲、乙两位同学的有2种结果,所以恰好选中甲、乙两位同学的概率为![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背最资料)
低碳生活的理念已逐步被人们所接受,据有关资料统计,一个人平均一年节约的用电相当于减排二氧化碳约18kg;一个人平均一年少买的衣服,相当于减排二氧化碳6kg.
(问题解决)
甲校对本校师生提出“节约用电”的倡议,乙校对本校师生提出“少买衣服”的倡议,2017年两校响应本校倡议的共有1000人,因此而减排二氧化碳总量约13200kg.问:2017年甲、乙两校响应倡议的人数分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】以∠AOB的顶点O为端点引射线OP,使∠AOP:∠BOP=3:2,若∠AOB=20°,则∠AOP的度数为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
我们知道,
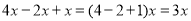 ,类似地,我们把
,类似地,我们把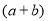 看成一个整体,则
看成一个整体,则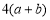
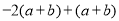 =
= .“整体思想”是初中数学解题中的一种重要的思想方法,它在多项式的化简与求职中应用极为广泛.
.“整体思想”是初中数学解题中的一种重要的思想方法,它在多项式的化简与求职中应用极为广泛.尝试应用:
(1)把
 看成一个整体,合并
看成一个整体,合并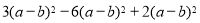 的结果为_______.
的结果为_______.(2)已知
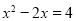 ,求
,求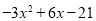 的值.
的值.拓广探索:
(3)已知
 ,求
,求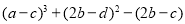 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.
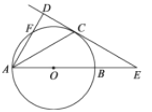
(1)求证:AD⊥CD;
(2)若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14,
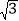 ≈1.73,结果保留一位小数.)
≈1.73,结果保留一位小数.) -
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价
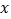 (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.(1)求年销售量
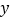 与销售单价
与销售单价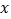 的函数关系式;
的函数关系式;(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,平行四边形ABCD的坐标分别为A(﹣1,0)、B(0,2)、C(4,2)、D(3,0),点P是AD边上的一个动点,若点A关于BP的对称点为A',则A'C的最小值为( )
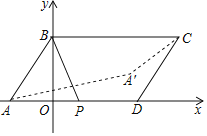
A.
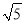 B.
B.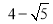 C.
C.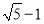 D.1
D.1
相关试题

