【题目】如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD.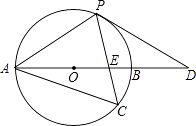
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若 ![]() :
: ![]() =1:2,求AE:EB:BD的值(请你直接写出结果);
=1:2,求AE:EB:BD的值(请你直接写出结果);
(3)若点C是弧AB的中点,已知AB=4,求CE ![]() CP的值.
CP的值.
参考答案:
【答案】
(1)解:PD与⊙O相切.理由如下:
连接OP,
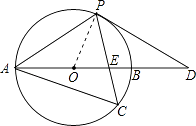
∵∠ACP=60°,
∴∠AOP=120°,
而OA=OP,
∴∠PAO=∠APO=30°,
∵PA=PD,
∴∠D=∠PAD=30°,
∴∠APD=180°﹣30°﹣30°=120°,
∴∠OPD=120°﹣30°=90°,
∵OP为半径,
∴PD是⊙O的切线;
(2)解:连BC,

∵AB为直径,
∴∠ACB=90°,
∵ ![]() :
: ![]() =1:2,
=1:2,
∴∠ABC=2∠BAC,
∴∠BAC=30°,∠ABC=60°,
而∠PAE=30°,
∴∠APE=∠DPE=60°,
∴AE垂直平分PC,如图,
设BE=x,在Rt△BCE中,∠BCE=30°,则BC=2BE=2x,
在Rt△ABC中,∠CAB=30°,AB=2BC=4x,
∴AE=AB﹣BE=3x,
∵PA=PD,PE⊥AD,
∴AE=DE,
∴DB=3x﹣x=2x,
∴AE:EB:BD的值为3:1:2
(3)解:如图,连接OC,

∵弧AC=弧BC,CO⊥AD,
∴∠CAB=∠APC,OC⊥AB,
而∠ACE=∠PCA,
∴△ACE∽△PCA,
∴ ![]() ,即AC2=PC
,即AC2=PC ![]() CE,
CE,
∵A02+OC2=AC2=8,
∴PC ![]() CE=AC2=8.
CE=AC2=8.
【解析】(1)连接OP,利用圆周角定理可求出∠AOP=120°,进而可得∠PAO=∠APO=30°,再利用等腰三角形的性质可求出∠D=30°,进而可得∠OPD=90°,从而得证;
(2)连BC,由AB为直径可得∠ACB=90°,再由已知可得∠BAC=30°,∠ABC=60°,从而得出AE垂直平分PC,设BE=x,在Rt△BCE和Rt△ABC中,利用直角三角形的性质可得答案;
(3)连接OC,由圆周角定理可得∠CAB=∠APC,OC⊥AB,从而证出△ACE∽△PCA,由相似三角形的性质可得AC2=PC ![]() CE,又由勾股定理可求出AC2,进而求出答案.
CE,又由勾股定理可求出AC2,进而求出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,∠AOB、∠COD都是直角.
(1)试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)若∠BOC=60°,求∠AOD的度数;
(3)猜想∠AOD与∠BOC在数量上是相等,互余,还是互补的关系,并说明理由;
(4)当∠COD绕着点O旋转到图(2)所示位置时,你在(3)中的猜想还成立吗?请用你所学的知识加以说明.
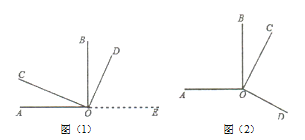
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点 D,E 分别在边 AC,AB 上,BD 与 CE 交于点 O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC 是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】运算能力是一项重要的数学能力.兵老师为帮助学生诊断和改进运算中的问题,对全班学生进行了三次运算测试(每次测验满分均为100分).小明和小军同学帮助兵老师统计了某数学小组5位同学(A,B,C,D,E,F)的三次测试成绩,小明在下面两个平面直角坐标系里描述5位同学的相关成绩.小军仔细核对所有数据后发现,图1中所有同学的成绩坐标数据完全正确,而图2中只有一个同学的成绩纵坐标数据有误.以下说法中:①A同学第一次成绩50分,第二次成绩40分,第三次成绩60分;②B同学第二次成绩比第三次成绩高;③D同学在图2中的纵坐标是有误的;④E同学每次测验成绩都在95分以上.其中合理的是( )

A.①②③B.①②④C.①③④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.

(1)当AC的长度为多少时,△AMC和△BOD相似;
(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;
(3)连结BC.当S△AMC=S△BOC时,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,菱形ABCD中,已知∠BAD=120°,∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC,CD于点E,F.
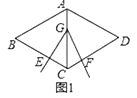
(1)如图2,当顶点G运动到与点A重合时,求证:EC+CF=BC;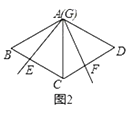
(2)知识探究:①如图3,当顶点G运动到AC中点时,探究线段EC,CF与BC的数量关系;
②在顶点G的运动过程中,若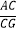 =t,请直接写出线段EC,CF与BC的数量关系(不需要写出证明过程);
=t,请直接写出线段EC,CF与BC的数量关系(不需要写出证明过程);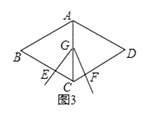
(3)问题解决:如图4,已知菱形边长为8,BG=7,CF=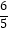 ,当t>2时,求EC的长度.
,当t>2时,求EC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(﹣2,0),(6,﹣8).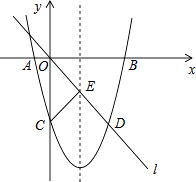
(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使△FOE≌△FCE?若存在,请直接写出点F的坐标;若不存在,请说明理由;
(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,试探究:当m为何值时,△OPQ是等腰三角形.
相关试题

