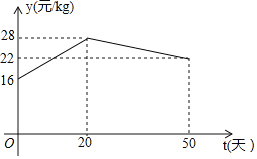
【题目】随着龙虾节的火热举办,某龙虾养殖大户为了发挥技术优势,一次性收购了10000kg小龙虾,计划养殖一段时间后再出售.已知每天养殖龙虾的成本相同,放养10天的总成本为166000,放养30天的总成本为178000元.设这批小龙虾放养t天后的质量为akg,销售单价为y元/kg,根据往年的行情预测,a与t的函数关系为a=![]() ,y与t的函数关系如图所示.
,y与t的函数关系如图所示.
(1)设每天的养殖成本为m元,收购成本为n元,求m与n的值;
(2)求y与t的函数关系式;
(3)如果将这批小龙虾放养t天后一次性出售所得利润为W元.问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大?最大利润是多少?
(总成本=放养总费用+收购成本;利润=销售总额﹣总成本)
参考答案:
【答案】(1)m=600,n=160000;(2)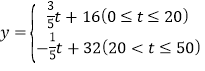 ;(3)该龙虾养殖大户将这批小龙虾放养25天后一次性出售所得利润最大,最大利润是108500元.
;(3)该龙虾养殖大户将这批小龙虾放养25天后一次性出售所得利润最大,最大利润是108500元.
【解析】(1)根据题意列出方程组,求出方程组的解得到m与n的值即可;
(2)根据图象,分类讨论利用待定系数法求出y与P的解析式即可;
(3)根据W=ya﹣mt﹣n,表示出W与t的函数解析式,利用一次函数与二次函数的性质求出所求即可.
(1)依题意得![]() ,
,
解得:![]() ;
;
(2)当0≤t≤20时,设y=k1t+b1,
由图象得:![]() ,
,
解得: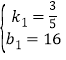
∴y=![]() t+16;
t+16;
当20<t≤50时,设y=k2t+b2,
由图象得:![]() ,
,
解得: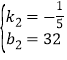 ,
,
∴y=﹣![]() t+32,
t+32,
综上, ;
;
(3)W=ya﹣mt﹣n,
当0≤t≤20时,W=10000(![]() t+16)﹣600t﹣160000=5400t,
t+16)﹣600t﹣160000=5400t,
∵5400>0,
∴当t=20时,W最大=5400×20=108000,
当20<t≤50时,W=(﹣![]() t+32)(100t+8000)﹣600t﹣160000=﹣20t2+1000t+96000=﹣20(t﹣25)2+108500,
t+32)(100t+8000)﹣600t﹣160000=﹣20t2+1000t+96000=﹣20(t﹣25)2+108500,
∵﹣20<0,抛物线开口向下,
∴当t=25,W最大=108500,
∵108500>108000,
∴当t=25时,W取得最大值,该最大值为108500元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到等式(a+b)2=a2+2ab+b2,请解各下列问题:
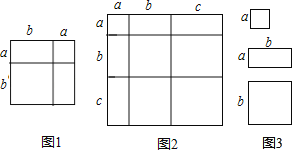
(1)写出图2中所表示的数学等式 .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出一个面积为(5a+7b)(9a+4b)长方形,则x= ,y= ,z= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学实践活动小组借助载有测角仪的无人机测量象山岚光阁与文明湖湖心亭之间的距离.如图,无人机所在位置P与岚光阁阁顶A、湖心亭B在同一铅垂面内,P与B的垂直距离为300米,A与B的垂直距离为150米,在P处测得A、B两点的俯角分别为α、β,且tanα=
 ,tanβ=
,tanβ=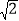 ﹣1,试求岚光阁与湖心亭之间的距离AB.(计算结果若含有根号,请保留根号)
﹣1,试求岚光阁与湖心亭之间的距离AB.(计算结果若含有根号,请保留根号)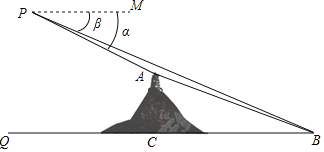
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

-
科目: 来源: 题型:
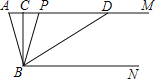
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,AD交⊙O于F,FM⊥AB于H,分别交⊙O、AC于M、N,连接MB,BC.
(1)求证:AC平分∠DAE;
(2)若cosM=
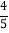 ,BE=1,①求⊙O的半径;②求FN的长.
,BE=1,①求⊙O的半径;②求FN的长.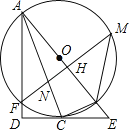
-
科目: 来源: 题型:
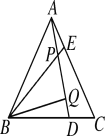
查看答案和解析>>【题目】如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:△ABE≌△CAD;
(2) 求BE的长
相关试题

