【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

参考答案:
【答案】(1)详见解析;(2)BD=CE,BD⊥CE.
【解析】
(1)通过边角边的证明方法找出相应的边角对应关系即可.
(2)根据第一问得大小关系,再求出∠DBC+∠DCB=90°即可得位置关系.
证明:(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
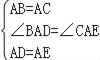 ,
,
∴△BAD≌△CAE(SAS).
(2)BD=CE,BD⊥CE,理由如下:
由(1)知,△BAD≌△CAE,
∴BD=CE;
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)
 =x﹣2;
=x﹣2;(2)
 =2
=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,P是第一象限角平分线上的一点,且P点的横坐标为3.把一块三角板的直角顶点固定在点P处,将此三角板绕点P旋转,在旋转的过程中设一直角边与x轴交于点E,另一直角边与y轴交于点F,若△POE为等腰三角形,则点F的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,cosA=
 ,D为AB上一点,且AD:BD=1:2,若BC=3
,D为AB上一点,且AD:BD=1:2,若BC=3  ,求CD的长.
,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
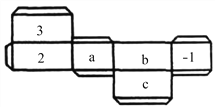
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)+4abc].
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(6,3)、B(6,0)在直角坐标系内.以原点O为位似中心,相似比为
 ,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )
,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为( )
A.(3,1)
B.(2,0)
C.(3,3)
D.(2,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”.根据题意可得CD的长为 .

相关试题

