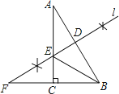
【题目】如图所示,在Rt△ABC中,∠C=90°,∠A=30°.
(1)尺规作图:作线段AB的垂直平分线l(保留作图痕迹,不写作法);
(2)在已作的图形中,若l分别交AB、AC及BC的延长线于点D、E、F,连接BE.求证:EF=2DE.

参考答案:
【答案】(1)见解析;(2)见解析。
【解析】
(1)根据垂直平分线的做法即可画出(2)根据垂直平分线的性质与含30°角的直角三角形的性质即可证明.
解:(1)直线l即为所求.
分别以AB为圆心,以任意长为半径,两圆相交于两点,连接此两点即可.作图正确.
(2)证明:在Rt△ABC中,∵∠A=30°,∠ABC=60°.
又∵l为线段AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=30°,∠AED=∠BED=60°,
∴∠EBC=30°=∠EBA,∠FEC=60°.
又∵ED⊥AB,EC⊥BC,
∴ED=EC.
在Rt△ECF中,∠FEC=60°,
∴∠EFC=30°,
∴EF=2EC,∴EF=2ED.
-
科目: 来源: 题型:
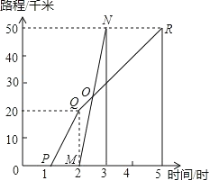
查看答案和解析>>【题目】如图所示 A、B 两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地.如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
(1)甲乙两人中, 先出发,先出发 小时.
(2)甲乙两人中, 先到达B地,先到 小时.
(3)分别求出乙骑摩托车的速度和甲骑自行车在全程的平均速度.
(4)乙出发大约用多长时间就追上甲?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;再以A3为圆心,1为半径向右画弧交OB于点A4,得第4条线段A3A4;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n的值是( )

A. 6B. 7C. 8D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.

求证:
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)若 ,求⊙O的半径。
,求⊙O的半径。 -
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到
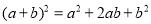 ,请解答下列问题:
,请解答下列问题:
(1)图2所表示的数学等式为_____________________;
(2)利用(1)得到的结论,解决问题: 若
 ,求
,求 的值;
的值;(3)如图3,将两个边长分别为a和b的正方形拼在一起,
 三点在同一直线上,连接
三点在同一直线上,连接 ,若两正方形的边长满足
,若两正方形的边长满足
 求阴影部分面积.
求阴影部分面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号汽车油箱容量为40L,每行驶100km耗油10L.设一辆加满油的该型号汽车行驶路程为x(km),行驶过程中油箱内剩余油量为y(L)
(1)求y与x之间的函数表达式;
(2)为了有效延长汽车使用寿命,厂家建议每次加油时油箱内剩余油量不低于油箱容量的四分之一,按此建议,求该辆汽车最多行驶的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA切⊙O于A,AB⊥OP于B,若PO=8 cm,BO=2 cm,则PA的长为( )

A.16cm
B.48cm
C.6 cm
cm
D.4 cm
cm
相关试题

