【题目】如图,△ABC是边长为4cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的是速度都为1厘米/秒.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(秒).
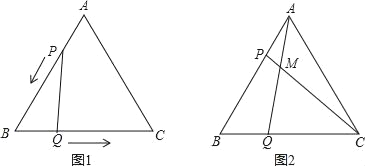
(1)当运动时间为t秒时,AP的长为 厘米,QC的长为 厘米;(用含t的式子表示)
(2)当t为何值时,△PBQ是直角三角形?
(3)连接AQ、CP,相交于点M,如图2,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
参考答案:
【答案】(1)t,4﹣t;(2)当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形;(3)∠CMQ=60°不变,理由见解析
秒时,△PBQ为直角三角形;(3)∠CMQ=60°不变,理由见解析
【解析】试题分析:(1)根据点P、Q的运动速度表示出AP、BQ的长,再根据BC的长即可表示出CQ的长;
(2)需要分类讨论:分∠PQB=90°和∠BPQ=90°两种情况;
(3)∠CMQ=60°不变.通过证△ABQ≌△CAP(SAS)得到:∠BAQ=∠ACP,所以由三角形外角定理得到∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°.
试题解析:(1)依题意得:AP=t,QC=4﹣t.
故答案是:t;4﹣t;
(2)设时间为t,则AP=BQ=t,PB=4﹣t,
①当∠PQB=90°时,
∵∠B=60°,
∴PB=2BQ,得4﹣t=2t,t=![]() ;
;
②当∠BPQ=90°时,
∵∠B=60°,
∴BQ=2BP,得t=2(4﹣t),t=![]() ;
;
∴当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形;
秒时,△PBQ为直角三角形;
(3)∠CMQ=60°不变.理由如下:
∵在△ABQ与△CAP中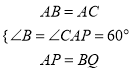 ,
,
∴△ABQ≌△CAP(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知□ABCD的面积为100,P为边CD上的任一点,E,F分别为线段AP,BP的中点,则图中阴影部分的总面积为( )

A. 30B. 25C. 22.5D. 20
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有七个数
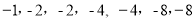 将它们填人图
将它们填人图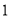 (
(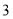 个圆两两相交分成
个圆两两相交分成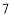 个部分)中,使得每个圆内部的
个部分)中,使得每个圆内部的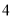 个数之积相等,设这个积为
个数之积相等,设这个积为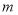 ,如图
,如图 给出了一种填法,此时
给出了一种填法,此时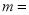 __________,在所有的填法中,
__________,在所有的填法中,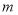 的最大值为__________.
的最大值为__________.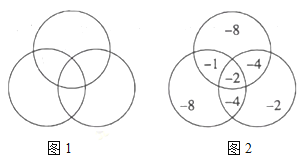
-
科目: 来源: 题型:
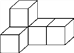
查看答案和解析>>【题目】用5个相同的正方体搭出如图所示的组合体.
(1)分别画出从正面、左面、上面看这个组合体时看到的图形;
(2)如果在这个组合体中,再添加一个相同的正方体组成一个新组合体,从正面、左面看这个新组合体时,看到的图形与原来相同.你认为这个设想能实现吗?若能,画出添加正方体后,从上面看这个组合体时看到的图形;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角△ABC中,AD是高,E,F分别是AB,AC中点,EF交AD于G,已知GF=1,AC= 6,△DEG的周长为10,则△ABC的周长为( )

A. 27-3
 B. 28-3
B. 28-3 C. 28-4
C. 28-4 D. 29-5
D. 29-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+2019x+m=0与x2+mx+2019=0有且只有一个公共根,m的值为( )
A. 2019B. -2019C. 2020D. -2020
相关试题

