【题目】如图,已知□ABCD的面积为100,P为边CD上的任一点,E,F分别为线段AP,BP的中点,则图中阴影部分的总面积为( )

A. 30B. 25C. 22.5D. 20
参考答案:
【答案】B
【解析】
先由△ABP与□ABCD同底等高,得出![]() ,再由中线的性质得到
,再由中线的性质得到![]() ,从而得到图中阴影部分的总面积.
,从而得到图中阴影部分的总面积.
∵平行四边形ABCD
∴S△ABP=![]() S平行四边形ABCD ,
S平行四边形ABCD ,
∴S△ADP+S△CBP+S△ABP=S平行四边形ABCD ,
∴S△ADP+S△CBP=![]() S平行四边形ABCD
S平行四边形ABCD
∵ E,F分别为线段AP,BP的中点,
∴S△ADE=![]() S△ADP , S△CBF=
S△ADP , S△CBF=![]() S△CBP
S△CBP
∴S△ADE+S△CBF=![]() (S△ADP+S△CBP)=
(S△ADP+S△CBP)=![]() S平行四边形ABCD=
S平行四边形ABCD=![]() ×100=25
×100=25
故答案为:B
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校为了了解我校七年级学生课外阅读的喜好,随机抽取我校七年级的部分学生进行问卷调查(每人只选一种书籍).下图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息回答问题:
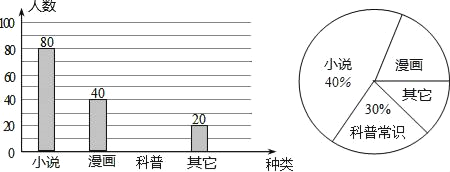
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,喜欢漫画的部分所占圆心角是 度;
(4)若七年级共有学生2800人,请你估计喜欢“科普常识”的学生人数共有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是杨辉三角系数表,它的作用是指导读者按规律写出行如(a+b)
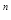 展开式的系数,请你仔细观察下表中的规律,填出展开式中所缺的系数。
展开式的系数,请你仔细观察下表中的规律,填出展开式中所缺的系数。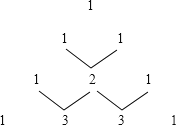
(1)、(a+b)=a+b
(2)、(a+b)
 =a
=a +2ab+b
+2ab+b
(3)、(a+b)
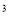 =a
=a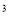 +3a
+3a b+3ab
b+3ab +b
+b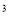
(4)、(a+b)
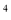 =a
=a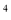 + a
+ a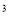 b+6a
b+6a b
b +4ab
+4ab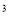 +b
+b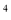
(5)(a+b)
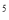 =a
=a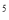 + a
+ a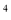 b+ a
b+ a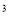 b
b + a
+ a b
b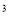 + ab
+ ab +b
+b
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列因式分解的过程,再回答所提出的问题:
1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]
=(1+x)2(1+x)
=(1+x)3
(1)上述分解因式的方法是 ,共应用了 次.
(2)若分解1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004,则需应用上述方法 次,结果是 .
(3)分解因式:1+x+x(x+1)+x(x+1)2+…+ x(x+1)n(n为正整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有七个数
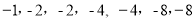 将它们填人图
将它们填人图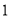 (
(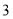 个圆两两相交分成
个圆两两相交分成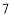 个部分)中,使得每个圆内部的
个部分)中,使得每个圆内部的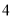 个数之积相等,设这个积为
个数之积相等,设这个积为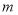 ,如图
,如图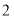 给出了一种填法,此时
给出了一种填法,此时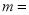 __________,在所有的填法中,
__________,在所有的填法中,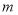 的最大值为__________.
的最大值为__________.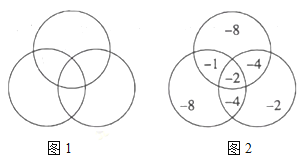
-
科目: 来源: 题型:
查看答案和解析>>【题目】用5个相同的正方体搭出如图所示的组合体.
(1)分别画出从正面、左面、上面看这个组合体时看到的图形;
(2)如果在这个组合体中,再添加一个相同的正方体组成一个新组合体,从正面、左面看这个新组合体时,看到的图形与原来相同.你认为这个设想能实现吗?若能,画出添加正方体后,从上面看这个组合体时看到的图形;若不能,说明理由.
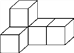
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为4cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的是速度都为1厘米/秒.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(秒).
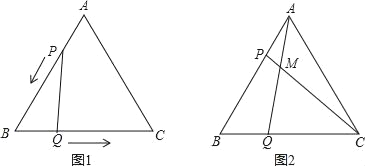
(1)当运动时间为t秒时,AP的长为 厘米,QC的长为 厘米;(用含t的式子表示)
(2)当t为何值时,△PBQ是直角三角形?
(3)连接AQ、CP,相交于点M,如图2,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
相关试题

