【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

参考答案:
【答案】(1)y=3x﹣30;(2)4月份上网20小时,应付上网费60元;(3)5月份上网35个小时.
【解析】
(1)由图可知,当x≥30时,图象是一次函数图象,设函数关系式为y=kx+b,使用待定系数法求解即可;
(2)根据题意,从图象上看,30小时以内的上网费用都是60元;
(3)根据题意,因为60<75<90,当y=75时,代入(1)中的函数关系计算出x的值即可.
(1)当x≥30时,设函数关系式为y=kx+b,
则![]() ,
,
解得![]() ,
,
所以y=3x﹣30;
(2)若小李4月份上网20小时,由图象可知,他应付60元的上网费;
(3)把y=75代入,y=3x-30,解得x=35,
∴若小李5月份上网费用为75元,则他在该月份的上网时间是35小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.
如:①用配方法分解因式:a2+6a+8,
解:原式=a2+6a+8+1-1=a2+6a+9-1
=(a+3)2-12=

②M=a2-2a-1,利用配方法求M的最小值.
解:
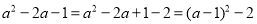
∵(a-b)2≥0,∴当a=1时,M有最小值-2.
请根据上述材料解决下列问题:
(1)用配方法因式分解:
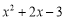 .
.(2)若
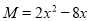 ,求M的最小值.
,求M的最小值.(3)已知x2+2y2+z2-2xy-2y-4z+5=0,求x+y+z的值.
-
科目: 来源: 题型:
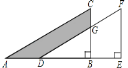
查看答案和解析>>【题目】如图,将直角三角形 ABC 沿 AB 方向平移 AD 的长度得到三角形DEF,已知BE=5, EF=8, CG=2,则图中阴影部分的面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A、B两种型号的空气净化器,两种净化器的销售相关信息见下表:
A型销售数量(台)
B型销售数量(台)
总利润(元)
5
10
2000
10
5
2500
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300m3/小时,B型空气净化器的净化能力为200m3/小时,某长方体室内活动场地的总面积为200m2 , 室内墙高3m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内就欧诺个气净化一新,若不考虑空气对流等因素,至少要购买A型空气净化器多少台? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
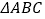 的
的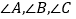 所对边分别是
所对边分别是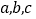 ,且
,且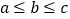 ,若满足
,若满足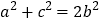 ,则称
,则称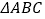 为奇异三角形,例如等边三角形就是奇异三角形.
为奇异三角形,例如等边三角形就是奇异三角形.(1)若
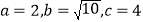 ,判断
,判断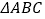 是否为奇异三角形,并说明理由;
是否为奇异三角形,并说明理由;(2)若
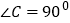 ,
,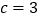 ,求
,求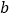 的长;
的长;(3)如图2,在奇异三角形
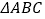 中,
中,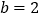 ,点
,点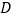 是
是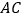 边上的中点,连结
边上的中点,连结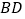 ,
,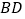 将
将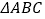 分割成2个三角形,其中
分割成2个三角形,其中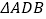 是奇异三角形,
是奇异三角形,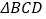 是以
是以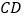 为底的等腰三角形,求
为底的等腰三角形,求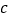 的长.
的长.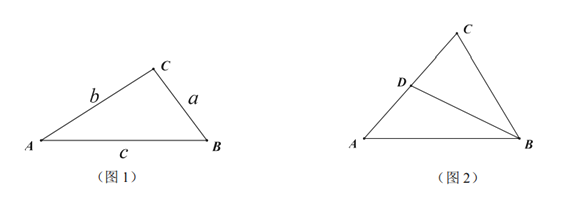
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.
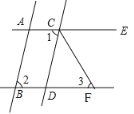
(1)试判断直线AE与BF有怎样的位置关系,并说明理由;
(2)若∠1=80°,求∠3的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题发现:如图1,在△ABC中,∠C=90°,分别以AC、BC为边向外侧作正方形ACDE和正方形BCFG.

(1)△ABC与△DCF面积的关系是;(请在横线上填写“相等”或“不相等”)
(2)拓展探究:若∠C≠90°,(1)中的结论还成立吗?若成立,请结合图2给出证明;若不成立,请说明理由;
(3)解决问题:如图3,在四边形ABCD中,AC⊥BD,且AC与BD的和为10,分别以四边形ABCD的四条边为边向外侧作正方形ABFE、正方形BCHG、正方形CDJI、正方形DALK,运用(2)的结论,图中阴影部分的面积和是否有最大值?如果有,请求出最大值,如果没有,请说明理由.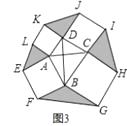
相关试题

