【题目】如图,锐角△ABC中,AD是高,E,F分别是AB,AC中点,EF交AD于G,已知GF=1,AC= 6,△DEG的周长为10,则△ABC的周长为( )

A. 27-3![]() B. 28-3
B. 28-3![]() C. 28-4
C. 28-4![]() D. 29-5
D. 29-5![]()
参考答案:
【答案】C
【解析】
由中点性质先得AF=3,再用勾股定理求出AG=2![]() ,然后由中位线性质得DG=AG=2
,然后由中位线性质得DG=AG=2![]() ,已知△DEG的周长为10,所以求得EG+DE的值,进一步证得AB=2DE,BD=2EG,从而求得△ABC的周长.
,已知△DEG的周长为10,所以求得EG+DE的值,进一步证得AB=2DE,BD=2EG,从而求得△ABC的周长.
∵ E,F分别是AB,AC中点,EF交AD于G,
∴EF∥BC,![]()
∵AD是高
∴∠ADC=∠AGF=90°
在Rt△AGF中
![]()
∵EF∥BC
∴![]()
∴FG是△ADC的中位线
∴DC=2GF=2
∴DG=AG=2![]()
∵ △DEG的周长为10,
∴EG+DE=10-2![]()
在Rt△ADB中,点E是AB边的中点,点G是AD的中点,
∴AB=2DE,BD=2EG
∴AB+BD=2(EG+DE)=20-4![]()
∴△ABC的周长为:AB+BD+DC+AC=20-4![]() +2+6=28-4
+2+6=28-4![]()
故答案为:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】用5个相同的正方体搭出如图所示的组合体.
(1)分别画出从正面、左面、上面看这个组合体时看到的图形;
(2)如果在这个组合体中,再添加一个相同的正方体组成一个新组合体,从正面、左面看这个新组合体时,看到的图形与原来相同.你认为这个设想能实现吗?若能,画出添加正方体后,从上面看这个组合体时看到的图形;若不能,说明理由.
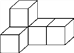
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为4cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的是速度都为1厘米/秒.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(秒).
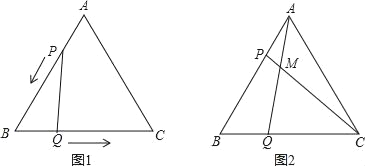
(1)当运动时间为t秒时,AP的长为 厘米,QC的长为 厘米;(用含t的式子表示)
(2)当t为何值时,△PBQ是直角三角形?
(3)连接AQ、CP,相交于点M,如图2,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+2019x+m=0与x2+mx+2019=0有且只有一个公共根,m的值为( )
A. 2019B. -2019C. 2020D. -2020
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止),此时的俯角为30°.为了便于观察,飞机继续向前飞行了800m到达B点,此时测得点F的俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A,B,C在同一直线上),竖直高度CF约为多少米?(结果保留整数.参考数据:
 ≈1.7)
≈1.7)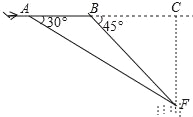
相关试题

