【题目】二次函数y=ax2+bx+c(a≠0)的图象经过点(-2,0),(x0,0),1<x0<2,与y轴的负半轴相交,且交点在(0,-2)的上方,下列结论:
①b>0;②2a<b;③2a-b-1<0;④2a+c<0.其中正确结论是 _________(填正确序号)
参考答案:
【答案】①③④
【解析】试题解析:根据题意可知①抛物线的开口向上,则![]()
对称轴在x轴的左侧,因此,a、b同号,则![]() 故①正确;
故①正确;
②∵抛物线交x轴与点(2,0)
∴4a2b+c=0,得![]()
,而2<c<0, ![]() 即
即![]()
故②错误;
③![]() 2ab1<0,故③正确;
2ab1<0,故③正确;
④∵把(2,0)代入![]() 得:4a2b+c=0,
得:4a2b+c=0,
∴即2b=4a+c>0(因为b>0),
∵当x=1时,a+b+c<0,
∴2a+2b+2c<0,
∴6a+3c<0,
即2a+c<0,∴④正确;
故答案为:①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实立德树人根本任务,培养德智体美劳全面发展的社会主义接班人,育才学校在设立学生奖学金时规定:每学期对学生的德智体美劳五个方面进行三次综合素质评价,分别是:假期综合素质评价、期中综合素质评价、期末综合素质评价,八年级(1)班的小明和八年级(2)班的小亮两位同学同时进入一等奖学金测评,他们的三次综合素质评价成绩如下表.
假期综合素质评价成绩
期中综合素质评价成绩
期末综合素质评价成绩
小明
96
91
92
小亮
95
93
91
(1)如果从三次综合素质评价成绩稳定性的角度来看,谁可以得一等奖学金?请你通过计算回答;
(2)如果假期综合素质评价成绩、期中综合素质评价成绩、期末综合素质评价成绩按
 的比例计入最终成绩,谁可以得一等奖学金?请你通过计算回答.
的比例计入最终成绩,谁可以得一等奖学金?请你通过计算回答. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,直线y=﹣x﹣3与x轴交于点A,与y轴交于点C,抛物线y=x2+bx+c经过A、C两点,与x轴交于另一点B
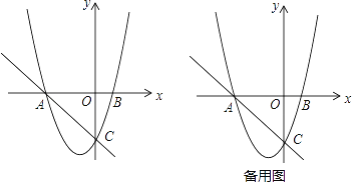
(1)求抛物线的解析式;
(2)点D是第二象限抛物线上的一个动点,连接AD、BD、CD,当S△ACD=
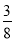 S四边形ACBD时,求D点坐标;
S四边形ACBD时,求D点坐标; (3)在(2)的条件下,连接BC,过点D作DE⊥BC,交CB的延长线于点E,点P是第三象限抛物线上的一个动点,点P关于点B的对称点为点Q,连接QE,延长QE与抛物线在A、D之间的部分交于一点F,当∠DEF+∠BPC=∠DBE时,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
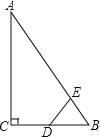
A.2B.2.5或3.5
C.3.5或4.5D.2或3.5或4.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】1979年,在邓小平同志的提议下,第五届全国人大常委会第六次会议决定每年3月12日为我国的植树节,今年是第40个植树节,明德中学师生积极响应国家“绿水青山就是金山银山”的号召,到距学校20千米的山上义务植树,老师和男生骑自行车先走,走了16千米后,女生乘汽车拉着工具、树苗出发,结果同时到达.已知汽车的速度比自行车的速度快60千米/小时,求两种车的速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
如图是一个正方形纸片
 ,如果将正方形纸片
,如果将正方形纸片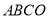 绕点
绕点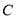 逆时针旋转角度
逆时针旋转角度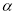
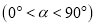 ,得到正方形
,得到正方形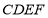 ,
,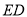 交
交 于点
于点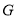 ,
,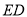 的延长线交
的延长线交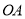 于点
于点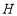 ,连接
,连接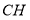 、
、 .
.
(1)求证:
 平分
平分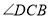 ;
;(2)直接写出线段
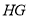 、
、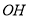 、
、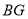 之间的数量关系;
之间的数量关系;(3)连接
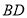 ,
,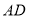 ,
, ,
,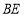 ,试探究在旋转过程中,四边形
,试探究在旋转过程中,四边形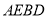 能否成为矩形?请说明理由.
能否成为矩形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】新知探究: 光在反射时,光束的路径可用图(1)来表示.
 叫做入射光线,
叫做入射光线, 叫做反射光线,从入射点
叫做反射光线,从入射点 引出的一条垂直于镜面
引出的一条垂直于镜面 的射线
的射线 叫做法线.
叫做法线.  与
与 的夹角
的夹角 叫入射角,
叫入射角, 与
与 的夹角
的夹角 叫反射角.根据科学实验可得:
叫反射角.根据科学实验可得: .则图(1)中
.则图(1)中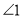 与
与 的数量关系是: 理由: ;
的数量关系是: 理由: ;问题解决: 生活中我们可以运用“激光”和两块相交的平面镜进行测距.如图(2)当一束“激光”
 射入到平面镜
射入到平面镜 上、被
上、被 反射到平面镜
反射到平面镜 上,又被平面镜
上,又被平面镜 反射后得到反射光线
反射后得到反射光线 .
.(1)若反射光线
 沿着入射光线
沿着入射光线 的方向反射回去,即
的方向反射回去,即 ,且
,且 ,则
,则
, 
 ;
;(2)猜想:当

 时,任何射到平面镜
时,任何射到平面镜 上的光线
上的光线 经过平面镜
经过平面镜 和
和 的两次反射后,入射光线
的两次反射后,入射光线 与反射光线
与反射光线 总是平行的.请你根据所学过的知识及新知说明.
总是平行的.请你根据所学过的知识及新知说明.
相关试题

