【题目】新知探究: 光在反射时,光束的路径可用图(1)来表示. ![]() 叫做入射光线,
叫做入射光线,![]() 叫做反射光线,从入射点
叫做反射光线,从入射点![]() 引出的一条垂直于镜面
引出的一条垂直于镜面![]() 的射线
的射线![]() 叫做法线.
叫做法线. ![]() 与
与![]() 的夹角
的夹角![]() 叫入射角,
叫入射角,![]() 与
与![]() 的夹角
的夹角![]() 叫反射角.根据科学实验可得:
叫反射角.根据科学实验可得:![]() .则图(1)中
.则图(1)中![]() 与
与![]() 的数量关系是: 理由: ;
的数量关系是: 理由: ;
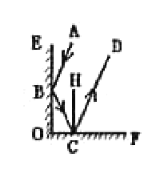
问题解决: 生活中我们可以运用“激光”和两块相交的平面镜进行测距.如图(2)当一束“激光”![]() 射入到平面镜
射入到平面镜![]() 上、被
上、被![]() 反射到平面镜
反射到平面镜![]() 上,又被平面镜
上,又被平面镜![]() 反射后得到反射光线
反射后得到反射光线![]() .
.
(1)若反射光线![]() 沿着入射光线
沿着入射光线![]() 的方向反射回去,即
的方向反射回去,即![]() ,且
,且![]() ,则
,则![]()
![]()
![]() ;
;
(2)猜想:当![]()
![]() 时,任何射到平面镜
时,任何射到平面镜![]() 上的光线
上的光线![]() 经过平面镜
经过平面镜![]() 和
和![]() 的两次反射后,入射光线
的两次反射后,入射光线![]() 与反射光线
与反射光线![]() 总是平行的.请你根据所学过的知识及新知说明.
总是平行的.请你根据所学过的知识及新知说明.

参考答案:
【答案】新知探究: ![]() , 等角的余角相等;问题解决:(1)
, 等角的余角相等;问题解决:(1)![]() ,
, ![]() ;(2)
;(2)![]() ,理由详见解析.
,理由详见解析.
【解析】
新知探究:利用等角的余角相等解决问题即可.
问题解决:(1)根据题意可求出∠CBO,从而得到∠ABC,然后根据平行线性质可求出∠BCD,从而得到∠BCO,最后利用三角形内角和定理可解决问题;
(2)过![]() 作
作![]() ,垂足为
,垂足为![]() ,根据题意和平行线性质可得
,根据题意和平行线性质可得![]() ,然后可证.
,然后可证.![]() ,问题得解.
,问题得解.
新知探究:∵∠α+∠1=90°,∠β+∠2=90°,∠α=∠β,
∴∠1=∠2(等角的余角相等),
故答案为:∠1=∠2,等角的余角相等;
问题解决:(1)由题意:∠ABE=∠CBO=35°,
∴∠ABC=110°,
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠BCD=70°,
∴∠BCO=∠DCF=55°,
∴∠O=180°35°55°=90°,
故答案为70°,90°;
(2)![]() ,
,
理由:如图,过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∵![]()
∴![]()
∴![]()
由题意知![]()
∴![]()
∴![]() ,
,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象经过点(-2,0),(x0,0),1<x0<2,与y轴的负半轴相交,且交点在(0,-2)的上方,下列结论:
①b>0;②2a<b;③2a-b-1<0;④2a+c<0.其中正确结论是 _________(填正确序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】1979年,在邓小平同志的提议下,第五届全国人大常委会第六次会议决定每年3月12日为我国的植树节,今年是第40个植树节,明德中学师生积极响应国家“绿水青山就是金山银山”的号召,到距学校20千米的山上义务植树,老师和男生骑自行车先走,走了16千米后,女生乘汽车拉着工具、树苗出发,结果同时到达.已知汽车的速度比自行车的速度快60千米/小时,求两种车的速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
如图是一个正方形纸片
 ,如果将正方形纸片
,如果将正方形纸片 绕点
绕点 逆时针旋转角度
逆时针旋转角度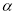
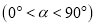 ,得到正方形
,得到正方形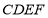 ,
,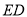 交
交 于点
于点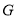 ,
,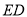 的延长线交
的延长线交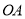 于点
于点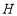 ,连接
,连接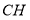 、
、 .
.
(1)求证:
 平分
平分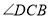 ;
;(2)直接写出线段
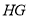 、
、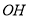 、
、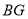 之间的数量关系;
之间的数量关系;(3)连接
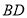 ,
,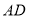 ,
, ,
,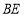 ,试探究在旋转过程中,四边形
,试探究在旋转过程中,四边形 能否成为矩形?请说明理由.
能否成为矩形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
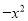 +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
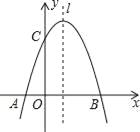
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
如图1,正比例函数
 的图象与反比例函数
的图象与反比例函数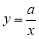 的图象交于点
的图象交于点 、
、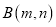 .我们可以发现:反比例函数
.我们可以发现:反比例函数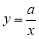 的图象是一个关于原点中心对称的图形.
的图象是一个关于原点中心对称的图形.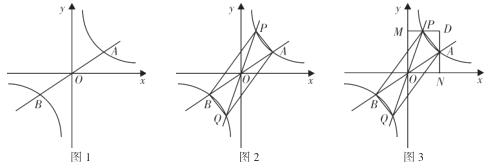
(1)填空:
 ,
,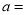 ,
,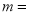 ,
, ;
;(2)利用所给函数图象,写出不等式
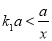 的解集 ;
的解集 ;(3)如图2,正比例函数
 的图象与反比例函数
的图象与反比例函数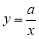 的图象交于点
的图象交于点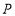 、
、 .试说明以
.试说明以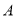 、
、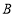 、
、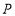 、
、 为顶点的四边形一定是平行四边形,但不可能是正方形;
为顶点的四边形一定是平行四边形,但不可能是正方形;(4)如图3,当点
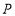 在点
在点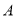 的左上方时,过
的左上方时,过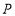 作直线
作直线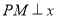 轴于点
轴于点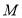 ,过点
,过点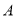 作直线
作直线轴于点
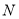 ,交直线
,交直线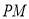 于点
于点 ,若四边形
,若四边形 的面积为
的面积为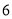 .求点
.求点 的坐标.
的坐标. -
科目: 来源: 题型:
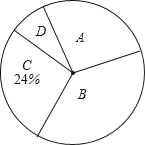
查看答案和解析>>【题目】某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06
(1)表中的a= ,b= ;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
相关试题

