【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、D在坐标轴上,其坐标分别为(2,0),(0,4),对角线AC⊥x轴. 
(1)求直线DC对应的函数解析式
(2)若反比例函数y= ![]() (k>0)的图象经过DC的中点M,请判断这个反比例函数的图象是否经过点B,并说明理由.
(k>0)的图象经过DC的中点M,请判断这个反比例函数的图象是否经过点B,并说明理由.
参考答案:
【答案】
(1)解:如图所示:过点D作DE⊥AC,垂足为E.

∵DE⊥AC,AC∥y轴,
∴∠EDO=90°.
∴∠EDA+∠ODA=90°.
又∵ABCD为矩形,
∴∠CDE+∠ADE=90°.
∴∠CDE=∠ODA.
又∵∠DOA=∠DEC=90°,
∴△DAO∽△DCE.
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得EC=1.
,解得EC=1.
∴C(2,5).
设直线DC的解析式为y=kx+4,将点C的坐标代入得:2k+4=5,解得k= ![]() .
.
∴直线CD的解析式为y= ![]() x+4
x+4
(2)解:过点D作DE⊥AC,过点B作BF⊥AC.

∵DE⊥AC,BF⊥AC.
∴∠DEC=∠BFA=90°.
∵DC∥AB,
∴∠DCE=∠FAB.
在△DEC和△BAF中  ,
,
∴△DEC≌△BAF.
∴DE=BF=2,EC=AF=1.
∴B(4,1).
∵D(0,4),C(2,5),
∴CD中点M的坐标为(1, ![]() ).
).
∴k=1× ![]() =
= ![]() .
.
∵4×1=4≠ ![]() ,
,
∴点B不在反比例函数图象上
【解析】过点D作DE⊥AC,垂足为E.先证明△DAO∽△DCE,依据相似三角形的性质可求得EC=1,从而可求得EC的长,故此可得到点C的坐标,设直线DC的解析式为y=kx+4,将点C的坐标代入求解即可;(2)过点D作DE⊥AC,过点B作BF⊥AC.先证明△DEC≌△BAF,从而可求得点B的坐标,然后再求得反比例反函数比例系数k的值,然后根据点B的坐标是否符合函数解析式进行判断即可.
【考点精析】通过灵活运用确定一次函数的表达式和矩形的性质,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为
 的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=
的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM= EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC=
 ,求乙的游泳速度.
,求乙的游泳速度. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产一种工具,据市场调查,若按每个工具280元销售时,每月可销售300个,若销售单价每降低1元,每月可多售出2个,据统计,每个工具的固定成本Q(元)与月销售y(个)满足如下关系:
月销量y(个)
100
160
240
320
每个工具的固定成本Q(元)
96
60
40
30
(1)写出月产销量y(个)与销售单价x(元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b在数轴上的对应点如图所示,则下列式子中错误的是( )

A. a+b<0 B. a-b<0
C. -a<-b D. |a-b|=b-a
-
科目: 来源: 题型:
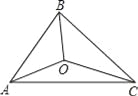
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于“倍根方程”的说法:①方程x2-3x+2=0是“倍根方程”;②若(x-2)(mx+n)=0是“倍根方程”,则4m2+5mn+n2=0;③若pq=2,则关于x的方程px2+3x+q=0是“倍根方程”;④若方程ax2+bx+c=0是“倍根方程”,且5a+b=0,则方程ax2+bx+c=0的一个根为
 .其中正确的是____(填序号).
.其中正确的是____(填序号).
相关试题

