【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于“倍根方程”的说法:①方程x2-3x+2=0是“倍根方程”;②若(x-2)(mx+n)=0是“倍根方程”,则4m2+5mn+n2=0;③若pq=2,则关于x的方程px2+3x+q=0是“倍根方程”;④若方程ax2+bx+c=0是“倍根方程”,且5a+b=0,则方程ax2+bx+c=0的一个根为![]() .其中正确的是____(填序号).
.其中正确的是____(填序号).
参考答案:
【答案】①②③
【解析】
①解得方程后即可利用倍根方程的定义进行判断;
②根据(x-2)(mx+n)=0是倍根方程,且x1=2,x2=-![]() 得到
得到![]() =-1,或
=-1,或![]() =-4,从而得到m+n=0,4m+n=0,进而得到4m2+5mn+n2=(4m+n)(m+n)=0正确;
=-4,从而得到m+n=0,4m+n=0,进而得到4m2+5mn+n2=(4m+n)(m+n)=0正确;
③已知条件pq=2,然后解方程px2+3x+q=0即可得到正确的结论;
④利用“倍根方程”的定义进行解答.
①解方程x2-3x+2=0得:x1=2,x2=1,
∴方程x2-3x+2=0是倍根方程,故①正确;
②∵(x-2)(mx+n)=0是倍根方程,且x1=2,x2=-![]() ,
,
∴![]() =-1,或
=-1,或![]() =-4,
=-4,
∴m+n=0,4m+n=0,
∵4m2+5mn+n2=(4m+n)(m+n)=0,故②正确;
③∵pq=2,
解方程px2+3x+q=0得:x1=-![]() ,x2=-
,x2=-![]() ,
,
∴x2=2x1,故③正确;
④∵方程ax2+bx+c=0是倍根方程,
∴设x1=2x2,
∴x1+x2=5,
∴x2+2x2=5,
∴x2=![]() ,故④错误.
,故④错误.
故答案是:①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、D在坐标轴上,其坐标分别为(2,0),(0,4),对角线AC⊥x轴.

(1)求直线DC对应的函数解析式
(2)若反比例函数y=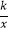 (k>0)的图象经过DC的中点M,请判断这个反比例函数的图象是否经过点B,并说明理由.
(k>0)的图象经过DC的中点M,请判断这个反比例函数的图象是否经过点B,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b在数轴上的对应点如图所示,则下列式子中错误的是( )

A. a+b<0 B. a-b<0
C. -a<-b D. |a-b|=b-a
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO= .
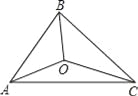
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求回答问题:
(1)发现
如图1,直线l1∥l2 , l1和l2的距离为d,点P在l1上,点Q在l2上,连接PQ,填空:PQ长度的最小值为.
(2)应用
如图2,在四边形ABCD中,DC∥AB,AD⊥AB,DC=2,AD=4,AB=6,点M在线段AD上,AM=3MD,点N在直线BC上,连接MN,求MN长度的最小值
(3)拓展
如图3,在四边形ABCD中,DC∥AB,AD⊥AB,DC=2,AD=4,AB=6,点M在线段AD上任意一点,连接MC并延长到点E,使MC=CE,以MB和ME为边作平行四边形MBNE,请直接写出线段MN长度的最小值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,其中点A在y轴的左侧,点C在x轴的下方,且OA=OC=5.
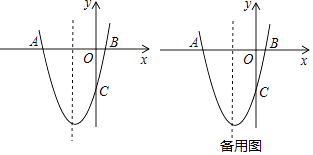
(1)求抛物线对应的函数解析式;
(2)点P为抛物线对称轴上的一动点,当PB+PC的值最小时,求点P的坐标;
(3)在(2)条件下,点E为抛物线的对称轴上的动点,点F为抛物线上的动点,以点P、E、F为顶点作四边形PEFM,当四边形PEFM为正方形时,请直接写出坐标为整数的点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,经过坐标原点的抛物线C1:y=ax2+bx与x轴的另一交点为M,它的顶点为点A,将C1绕原点旋转180°,得到抛物线C2 , C2与x轴的另一交点为N,顶点为点B,连接AM,MB,BN,NA,当四边形AMBN恰好是矩形时,则b的值( )
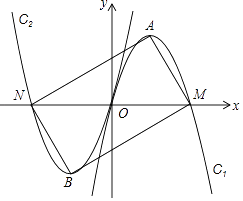
A.2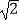
B.﹣2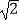
C.2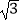
D.﹣2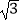
相关试题

