【题目】如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )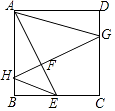
A.8
B.4 ![]()
C.2 ![]()
D.8 ![]()
参考答案:
【答案】C
【解析】如图,由题意易证AE=GH=2 ![]() ,设FH=x,EF=y,则有HE+AG=
,设FH=x,EF=y,则有HE+AG= ![]() +
+ ![]() ,
,
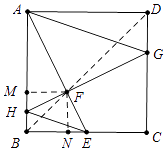
欲求HE+AG的最小值,相当于在平面直角坐标系内找一点(x,y),使得这个点到O(0,0),P(2 ![]() ,2
,2 ![]() )的距离和最小,显然这个点在线段OP上,满足x=y时,HE+AG的值最小,由此可知FH=EF时,HE+AG的值最小,如图连接BD交AE于F,作FM⊥AB于M,FN⊥BC于N,易证△FMH≌△FNE,
)的距离和最小,显然这个点在线段OP上,满足x=y时,HE+AG的值最小,由此可知FH=EF时,HE+AG的值最小,如图连接BD交AE于F,作FM⊥AB于M,FN⊥BC于N,易证△FMH≌△FNE,
∴FH=EF,此时HE+AG的值最小,
易证四边形BNFM是正方形,设边长为a,则有 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴a= ![]() ,
,
∴EF=FH= ![]() =
= ![]() ,
,
∴x=y= ![]() ,
,
∴HE+AG的最小值=2 ![]() ,
,
所以答案是:C.
解法二:作GK⊥AB于K,作EM∥AG,GM∥AE,则四边形AEGM是平行四边形.
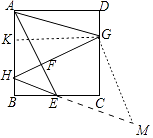
∵AE⊥HG,
∴∠B=∠GKH=∠AFH=90°,
∴∠BAE+∠AHF=90°,∠AHF+∠KGH=90°,
∴∠BAE=∠KGH,
∵KG=BC=AB,
∴△KGH≌△BAE,
∴GH=AG,
∴AE=GM=HG,AG=EM,
∴△GHM是等腰直角三角形,GH=GM=AE=2 ![]() ,
,
∵AG+HE=EM+EG,
∴当H、E、M共线时,AG+HE的值最小,最小值= ![]() HG=2
HG=2 ![]() .
.
所以答案是:C.
【考点精析】通过灵活运用正方形的性质和轴对称-最短路线问题,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④
 与EF相切;⑤EF∥MN.其中正确结论的个数是( )
与EF相切;⑤EF∥MN.其中正确结论的个数是( )
A.5个
B.4个
C.3个
D.2个 -
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角板按如图所示叠放在一起,若固定
 ,将
,将 绕着公共顶点
绕着公共顶点 ,按顺时针方向旋转
,按顺时针方向旋转 度
度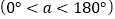 ,当
,当 的一边与
的一边与 的某一边平行时,相应的旋转角
的某一边平行时,相应的旋转角 的度数为_________________。
的度数为_________________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中,x与y的部分对应值如下表:
x
﹣3
﹣2
﹣1
0
y
0
﹣3
﹣4
﹣3
下列结论:
①ac<0;
②当x>1时,y随x的增大而增大;
③﹣4是方程ax2+(b﹣4)x+c=0的一个根;
④当﹣1<x<0时,ax2+(b﹣1)x+c+3>0.其中正确结论的个数为( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).

(1)试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;
(2)以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=2
 ,将扇形OAB沿过点B的直线折叠,点O恰好落在
,将扇形OAB沿过点B的直线折叠,点O恰好落在  上的点D处,折痕交OA于点C,则阴影部分的面积是 .
上的点D处,折痕交OA于点C,则阴影部分的面积是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,∠MON=80°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围.

(2)两条相交的直线OX、OY,使∠XOY=n,在射线OX、OY上分别再任意取A、B两点,作∠ABY的平分线BD,BD的反向延长线交∠OAB的平分线于点C,随着点A、B位置的变化,∠C的大小是否会变化?若保持不变,请求出∠C的度数;若发生变化,求出变化范围.

相关试题

