【题目】(1)如图,∠MON=80°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围.

(2)两条相交的直线OX、OY,使∠XOY=n,在射线OX、OY上分别再任意取A、B两点,作∠ABY的平分线BD,BD的反向延长线交∠OAB的平分线于点C,随着点A、B位置的变化,∠C的大小是否会变化?若保持不变,请求出∠C的度数;若发生变化,求出变化范围.

参考答案:
【答案】(1)∠APB的大小不变;∠APB=130°;(2)∠C的大小不变;∠C=![]() .
.
【解析】
(1)根据角平分线的定义得到∠OAC=∠BAC,∠OBD=∠ABD,进而由三角形的内角和得到2x+2y=100°,即x+y=50°,再根据三角形内角和是180°即可求解;
(2)令∠OAC=∠CAB=x,∠ABD=∠BDY=y,再根据三角形的外角性质即可求解.
解:(1)∵AC,BD平分∠OAB与∠OBA
∴∠OAC=∠BAC,∠OBD=∠ABD,
设∠OAC=∠BAC=x,∠OBD=∠ABD=y,
∵∠MON =80°
∴由内角和定理得2x+2y=100°
∴x+y=50°
∵∠APB=180°-(x+y)
∴∠APB=130°
∴∠APB的大小不变.
(2)由题意,设∠CAO=∠CAB=x,∠ABD=∠DBY=y,
∵∠ABY是△AOB的外角,
∴2y= n +2x,
同理,∠ABD是△ABC的外角,则y=∠C+x,
∴∠C=![]() ,所以∠C的大小不变.
,所以∠C的大小不变.
-
科目: 来源: 题型:
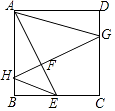
查看答案和解析>>【题目】如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )
A.8
B.4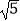
C.2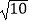
D.8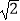
-
科目: 来源: 题型:
查看答案和解析>>【题目】方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).

(1)试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;
(2)以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=2
 ,将扇形OAB沿过点B的直线折叠,点O恰好落在
,将扇形OAB沿过点B的直线折叠,点O恰好落在  上的点D处,折痕交OA于点C,则阴影部分的面积是 .
上的点D处,折痕交OA于点C,则阴影部分的面积是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)已知:如图,△ABC中,D是AB的中点,E是AC上一点,EF∥AB,DF∥BE.
(1)猜想:DF与AE的关系是______.
(2)试说明你猜想的正确性.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:
①若通话时间少于120分,则A方案比B方案便宜20元;
②若通话时间超过200分,则B方案比A方案便宜12元;
③若通讯费用为60元,则B方案比A方案的通话时间多;
④若两种方案通讯费用相差10元,则通话时间是145分或185分.其中正确结论的序号是 .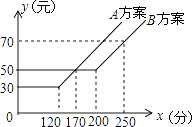
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=4cm,BE=5cm,点E是AD边上的一点,AE、DE分别长acm.bcm,满足(a-3)2+|2a+b-9|=0.动点P从B点出发,以2cm/s的速度沿B→C→D运动,最终到达点D,设运动时间为t s.
(1)a=______cm,b=______cm;
(2)t为何值时,EP把四边形BCDE的周长平分?
(3)另有一点Q从点E出发,按照E→D→C的路径运动,且速度为1cm/s,若P、Q两点同时出发,当其中一点到达终点时,另一点随之停止运动.求t为何值时,△BPQ的面积等于6cm2.


相关试题

