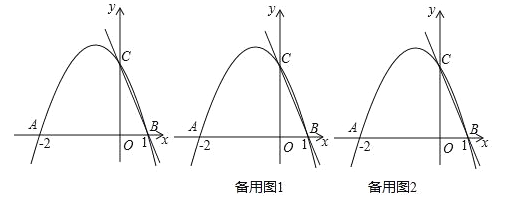
【题目】如图，二次函数y=ax2+bx+c的图象交x轴于A（﹣2，0），B（1，0），交y轴于C（0，2）．

（1）求二次函数的解析式；

（2）连接AC，在直线AC上方的抛物线上是否存在点N，使△NAC的面积最大，若存在，求出这个最大值及此时点N的坐标，若不存在，说明理由；

（3）若点M在x轴上，是否存在点M，使以B、C、M为顶点的三角形是等腰三角形，若存在，直接写出点M的坐标；若不存在，说明理由；

（4）若P为抛物线上一点，过P作PQ⊥BC于Q，在y轴左侧的抛物线是否存在点P使△CPQ∽△BCO（点C与点B对应），若存在，求出点P的坐标，若不存在，说明理由．

参考答案：

【答案】（1）y=﹣x2﹣x+2；（2）N（﹣1，2），△ANC的面积有最大值为1；（3）M的坐标为（﹣1，0）或（，0）或（，0）；（4）点P的坐标为：（﹣1，2）或（， ）．

【解析】试题分析：（1）利用交点式求二次函数的解析式；

（2）求直线AC的解析式，作辅助线ND，根据抛物线的解析式表示N的坐标，根据直线AC的解析式表示D的坐标，表示ND的长，利用铅直高度与水平宽度的积求三角形ANC的面积，根据二次函数的最值可得面积的最大值，并计算此时N的坐标；

（3）分三种情况：当B、C、M为顶点的三角形是等腰三角形时，分别以三边为腰，画图形，求M的坐标即可；

（4）存在两种情况：①如图4，点P1与点C关于抛物线的对称轴对称时符合条件；

②如图5，图3中的M（﹣，0）时，MB=MC，设CM与抛物线交于点P2，则△CP2Q∽△BCO，P2为直线CM的抛物线的交点．

试题解析：

解：（1）∵二次函数y=ax2+bx+c的图象交x轴于A（﹣2，0），B（1，0），

设二次函数的解析式为：y=a（x+2）（x﹣1），

把C（0，2）代入得：2=a（0+2）（0﹣1），

a=﹣1，

∴y=﹣（x+2）（x﹣1）=﹣x2﹣x+2，

∴二次函数的解析式为：y=﹣x2﹣x+2.

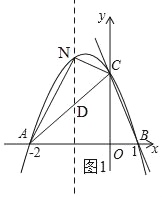
（2）如图1，过N作ND∥y轴，交AC于D，设N（n，﹣n2﹣n+2），

设直线AC的解析式为：y=kx+b，

把A（﹣2，0）、C（0，2）代入得： ，

解得： ，

∴直线AC的解析式为：y=x+2，

∴D（n，n+2），

∴ND=（﹣n2﹣n+2）﹣（n+2）=﹣n2﹣2n，

∴S△ANC=×2×[﹣n2﹣2n]=﹣n2﹣2n=﹣（n+1）2+1，

∴当n=﹣1时，△ANC的面积有最大值为1，此时N（﹣1，2），

（3）存在，分三种情况：

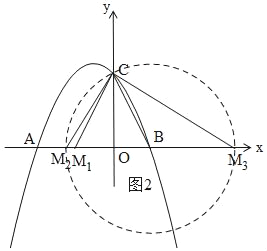
①如图2，当BC=CM1时，M1（﹣1，0）.

②如图2，由勾股定理得：BC==，

以B为圆心，以BC为半径画圆，交x轴于M2、M3，则BC=BM2=BM3=，

此时，M2（1﹣，0），M3（1+，0）.

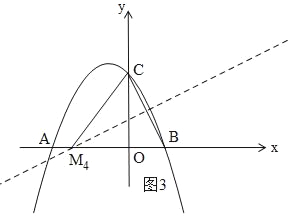
③如图3，作BC的中垂线，交x轴于M4，连接CM4，则CM4=BM4，

设OM4=x，则CM4=BM4=x+1，

由勾股定理得：22+x2=（1+x）2，

解得：x=，

∵M4在x轴的负半轴上，

∴M4（﹣，0），

综上所述，当B、C、M为顶点的三角形是等腰三角形时，M的坐标为（﹣1，0）或（1±，0）或（﹣，0）.

（4）存在两种情况：

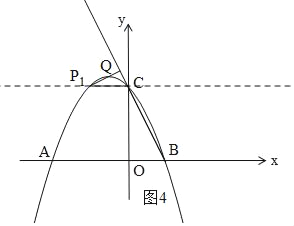
①如图4，过C作x轴的平行线交抛物线于P1，过P1作P1Q⊥BC，

此时，△CP1Q∽△BCO，

∴点P1与点C关于抛物线的对称轴对称，

∴P1（﹣1，2），

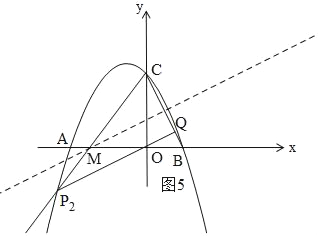
②如图5，由（3）知：当M（﹣，0）时，MB=MC，设CM与抛物线交于点P2，

过P2作P2Q⊥BC，此时，△CP2Q∽△BCO，

易得直线CM的解析式为：y=x+2，

则，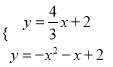

解得：P2（﹣，﹣），

综上所述，点P的坐标为：（﹣1，2）或（﹣，﹣）．

关闭