搜索
【题目】沭阳修远中学初二年级为响应政府在新冠肺炎疫情稳定之后及时复工复产的号召，计划开学之前用3000元购进A、B两种医用口罩共1100个，购买A种医用口罩与购买B种医用口罩的费用相同．已知A种医用口罩的单价是B种医用口罩单价的1.2倍．
（1）求A、B两种医用口罩的单价各是多少？
（2）若初三年级需要购买A、B两种医用口罩共2000个，其中购买A种口罩a个（
），设购买两种口罩总费用为w元，求w与a之间的函数关系式，并求出w的最小值．
参考答案：
【答案】（1）A 的单价是3元，B的单价是2.5元；（2） 
，最小为5400
【解析】
（1）根据用3000元购进A、B两种医用口罩共1100个，购买A种医用口罩与购买B种医用口罩的费用相同．已知A种医用口罩的单价是B种医用口罩单价的1.2倍．设出A、B两种医用口罩的单价列方程即可．
（2）根据A口罩数量为a，则B口罩数量为（2000-a）个，列出一次函数表达式根据a的取值范围求解即可．
解：（1）依题意设A 口罩的单价是1.2x元，B口罩的单价为x元，因为购买A种医用口罩与购买B种医用口罩的费用相同，所以费用均为3000
2=1500，
由题意列方程组为：
，
解得： x=2.5，
经检验x=2.5是方程的根
∴1.2x=3
答：A 口罩的单价是3元，B口罩的单价为2.5元；
（2）已知A口罩共a个，则B口罩有（2000-a）个，在（1）的结果下列表达式为：
W=3a+2.5（2000-a），化简为，
又∵
，
由一次函数性质知a=800时，W最小，即
，
即最小值为5400．
-
科目： 来源： 题型：
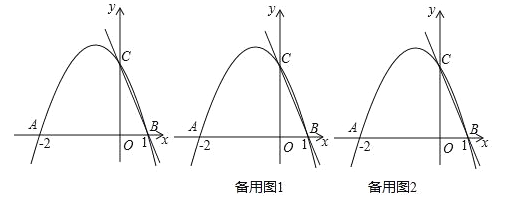
查看答案和解析>>【题目】如图，二次函数y=ax2+bx+c的图象交x轴于A（﹣2，0），B（1，0），交y轴于C（0，2）．
（1）求二次函数的解析式；
（2）连接AC，在直线AC上方的抛物线上是否存在点N，使△NAC的面积最大，若存在，求出这个最大值及此时点N的坐标，若不存在，说明理由；
（3）若点M在x轴上，是否存在点M，使以B、C、M为顶点的三角形是等腰三角形，若存在，直接写出点M的坐标；若不存在，说明理由；
（4）若P为抛物线上一点，过P作PQ⊥BC于Q，在y轴左侧的抛物线是否存在点P使△CPQ∽△BCO（点C与点B对应），若存在，求出点P的坐标，若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；
②方程
的两个根是x1=﹣1，x2=3；③3a+c＞0
④当y＞0时，x的取值范围是﹣1≤x＜3
⑤当x＜0时，y随x增大而增大
其中结论正确的个数是（ ）
A. 4个 B. 3个 C. 2个 D. 1个
-
科目： 来源： 题型：
查看答案和解析>>【题目】列方程组解应用题
5月份，甲、乙两个工厂用水量共为200吨．进入夏季用水高峰期后，两工厂积极响应国家号召，采取节水措施.6月份，甲工厂用水量比5月份减少了15%，乙工厂用水量比5月份减少了10%，两个工厂6月份用水量共为174吨，求两个工厂5月份的用水量各是多少?
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：通过小学的学习我们知道，分数可分为“真分数”和“假分数”．而假分数都可化为带分数，如：
．我们定义：在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．如：
，
这样的分式就是假分式；再如：
，
这样的分式就是真分式．类似的，假分式也可以化为带分式（即：整式与真分式的和的形式）．如：
；再如：
．解决下列问题：
（1）分式
是_____分式（填“真分式”或“假分式”）；（2）把假分式
化为带分式的形式（写出过程）；（3）如果分式
的值为整数，那么
的整数值为_____． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，圆心都在x轴正半轴上的半圆O1，半圆O2，…，半圆On与直线l相切．设半圆O1，半圆O2，…，半圆On的半径分别是r1，r2，…，rn，则当直线l与x轴所成锐角为30°，且r1＝1时，r2018＝_________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AB=DC，E、F分别是AD、BC的中点，G、H分别是对角线BD、AC的中点．
（1）求证：四边形EGFH是菱形；
（2）若AB=1，则当∠ABC+∠DCB=90°时，求四边形EGFH的面积．
相关试题
