【题目】如图1,已知⊙O的半径为1,∠PAQ的正切值为![]() ,AQ是⊙O的切线,将⊙O从点A开始沿射线AQ的方向滚动,切点为A'.
,AQ是⊙O的切线,将⊙O从点A开始沿射线AQ的方向滚动,切点为A'.
(1)sin∠PAQ= ,cos∠PAQ= ;
(2)①如图1,当⊙O在初始位置时,圆心O到射线AP的距离为 ;
②如图2,当⊙O的圆心在射线AP上时,AA'= ;
(3)在⊙O的滚动过程中,设A与A'之间的距离为m,圆心O到射线AP的距离为n,求n与m之间的函数关系式,并探究当m分别在何范围时,⊙O与射线AP相交、相切、相离.

参考答案:
【答案】(1)![]() ,
, ![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)n=
;(3)n= ,当0≤m<
,当0≤m<![]() 时,⊙O与AN相交,当m=
时,⊙O与AN相交,当m=![]() 时,⊙O与AN相切,当m>
时,⊙O与AN相切,当m>![]() 时,⊙O与AN相离.
时,⊙O与AN相离.
【解析】试题分析:(1)依据锐角三角函数的定义可求得sin∠PAQ、cos∠PAQ的值;
(2)①过点O作OB⊥AP,垂足为B.依据同角的余角相等可证明∠AOB=∠QAP,然后依据锐角三角函数的定义可求得OB的长;②连接OA′.由切线的性质可知∠OA′A=90°,接下来,依据锐角三角函数的定义可求得AA′的长;
(3)当0<m<2![]() 时,如图3所示:连接OA′,过点O作OH⊥AP,垂足为H.在Rt△OGH中,在Rt△AA′G中,依据锐角三角函数的定义可得到OG=
时,如图3所示:连接OA′,过点O作OH⊥AP,垂足为H.在Rt△OGH中,在Rt△AA′G中,依据锐角三角函数的定义可得到OG=![]() n、GA′=
n、GA′=![]() m,然后依据OG+GA′=1可得到n与m之间的函数关系式;当m>2
m,然后依据OG+GA′=1可得到n与m之间的函数关系式;当m>2![]() 时,如图2所示,过点O作OH⊥AP,垂足为H,连接A′O并延长交AP与点G.依据锐角三角函数的定义可知OG=
时,如图2所示,过点O作OH⊥AP,垂足为H,连接A′O并延长交AP与点G.依据锐角三角函数的定义可知OG=![]() n、,GA′=
n、,GA′=![]() m,由GA′﹣OG=1可得到n与m之间的函数关系式;接下来,依据d和r的关系可求得当直线AP与⊙O相切,相交、相离时m的取值范围.
m,由GA′﹣OG=1可得到n与m之间的函数关系式;接下来,依据d和r的关系可求得当直线AP与⊙O相切,相交、相离时m的取值范围.
试题解析:
解:(1)∵∠PAQ的正切值为![]() ,
,
∴sin∠PAQ= =
=![]() ,cos∠QAQ=
,cos∠QAQ= =
=![]() .
.
故答案为: ![]() ,
,![]() .
.
(2)①如图1所示:过点O作OB⊥AP,垂足为B.

∵AQ是⊙O的切线,
∴OA⊥AQ,
∴∠OAP+∠PAQ=90°,
∵OB⊥AP,
∴∠OAP+∠AOB=90°,
∴∠AOB=∠PAQ,
∴![]() =cos∠PAQ=
=cos∠PAQ=![]() ,
,
∵OA=1,
∴OB=![]() ,
,
∴圆心O到射线AP的距离为![]() .
.
②如图2所示:连接OA′,

∵⊙O与AQ相切,
∴OA′⊥AQ,
∴∠OA′A=90°,
∴![]() =tan∠A,
=tan∠A,
∴AA′=2![]() .
.
故答案为:2![]() .
.
(3)当0≤x≤2![]() 时,如图3所示:连接OA′,过点O作OH⊥AP,垂足为H.
时,如图3所示:连接OA′,过点O作OH⊥AP,垂足为H.

∵在Rt△OGH中,cos∠O=![]() =
=![]() ,
,
∴OG=![]() n,
n,
∵在Rt△AA′G中,tan∠A=![]() =
=![]() ,
,
∴GA′=![]() m,
m,
∵OG+GA′=1,
∴![]() n+
n+![]() m=1,
m=1,
∴n=﹣![]() m+
m+![]() .
.
②当x>2![]() 时,如图2所示,过点O作OH⊥AP,垂足为H,连接A′O并延长交AP与点G.
时,如图2所示,过点O作OH⊥AP,垂足为H,连接A′O并延长交AP与点G.

∵∠HGO=∠AGA′,∠GA′A=∠OHD=90°,
∴∠HOG=∠PAQ,
∴OG=![]() n,GA′=
n,GA′=![]() m,
m,
由GA′﹣OG=1得,n=![]() m-
m- ![]() ,
,
综上所述,n与m的函数关系式为n= .
.
∵当n=1时,⊙O与AP相切,此时![]() m-
m- ![]() =1,解得m=
=1,解得m=![]() +
+![]() ,
,
∴当0≤m<![]() +
+![]() 时,⊙O与AN相交,
时,⊙O与AN相交,
当m=![]() +
+![]() 时,⊙O与AN相切;
时,⊙O与AN相切;
当m>![]() +
+![]() 时,⊙O与AN相离.
时,⊙O与AN相离.
-
科目: 来源: 题型:
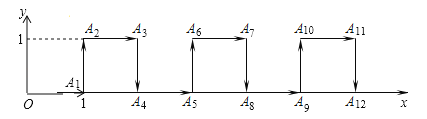
查看答案和解析>>【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )
A. 504m2 B.
 m2 C.
m2 C. 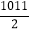 m2 D. 1009m2
m2 D. 1009m2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,C在OB的延长线上,D为⊙O上一点,∠BAD=∠BDC.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为1,且OB=BC,求四边形AOBD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】初二年级为了了解学生上学的交通方式,现从初二年级学生中随机抽取了部分学生进行“我上学的交通方式”问卷调査,规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项,并将统计结果绘制了如下两幅不完整的统计图.

请解答下列问题:
(1)在这次调査中,一共抽样调査了 名学生;
(2)扇形统计图中骑车所在扇形的圆心角的度数为 °;
(3)补全条形统计图;
(4)若初二年级共有1500名学生,试估计初二年级学生中选择“步行”方式的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,
, 的平分线与
的平分线与 的平分线交于点
的平分线交于点 ,则
,则 的度数是________.
的度数是________.
-
科目: 来源: 题型:
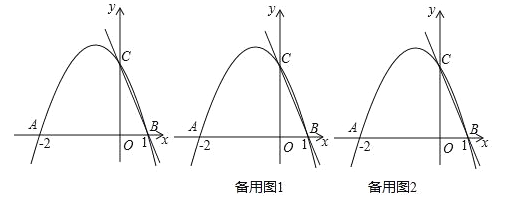
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣2,0),B(1,0),交y轴于C(0,2).
(1)求二次函数的解析式;
(2)连接AC,在直线AC上方的抛物线上是否存在点N,使△NAC的面积最大,若存在,求出这个最大值及此时点N的坐标,若不存在,说明理由;
(3)若点M在x轴上,是否存在点M,使以B、C、M为顶点的三角形是等腰三角形,若存在,直接写出点M的坐标;若不存在,说明理由;
(4)若P为抛物线上一点,过P作PQ⊥BC于Q,在y轴左侧的抛物线是否存在点P使△CPQ∽△BCO(点C与点B对应),若存在,求出点P的坐标,若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;
②方程
 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
相关试题

