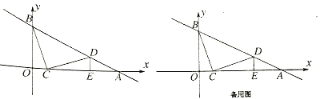
【题目】如图,在平面直角坐标系中,直线 y=kx+b与x 轴、y 轴相交干A(6,0),B(0,3)两点,动点C在线段OA上,将线段CB 绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D 作DE⊥x 轴于点E
(1)求直线y=kx+b 的表达式及点D 的坐标;
(2)若点P在y 轴上,点Q在直线AB上,是否存在以C、D、P、Q 为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q 点坐标,若不存在,请说明理由.
参考答案:
【答案】(1)D(4,1);(2)Q的坐标为![]()
![]() 或
或![]()
【解析】
(1)用待定系数法先求出直线解析式,由旋转角为90°,可证得∠BCO=∠CDE,从而得到△BOC≌△CED,所以OC=DE,BO=CE=3,设OC=DE=m, 则点D(m+3,m),代入解析式求出m,进而得到点D的坐标.(2)分三种情况画出图形,结合平行四边形的性质求出点的坐标即可.
解:
(1)将A(6,0)、B(0,3)代入直线y=kx+b得,
![]()
∴
![]() ,
,
∵∠BOC=∠BCD=∠CED=90°,
∴∠OCB+∠DCE=90°,∠DCE+∠CDE=90°,
∴∠BCO=∠CDE,
∵BC=CD,
∴△BOC≌△CED,
∴OC=DE,BO=CE=3,
设OC=DE=m,
∴D(m+3,m)
把D(m+3,m)代入![]() 得,
得,
![]() ,
,
∴m=1 ,
∴D(4,1),
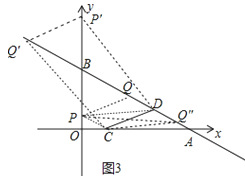
(2)如图,①作CP∥AB交y轴于P,作PQ∥CD交AB于Q,则四边形PCDQ是平行四边形,设![]() ,将C(1,0)代入得,b=
,将C(1,0)代入得,b=![]() ,
,
∴![]() ,
,
∴P(0,![]() ),
),
∵点C向右平移3个单位,再向上平移1个单位得到D,
∴点P向右平移3个单位,再向上平移1个单位得到Q,
∴Q![]()
② 作P′Q′∥CD交y轴于P′,交AB于Q′,则四边形Q′CDP′是平行四边形,
∵PQ![]() CD,P′Q′
CD,P′Q′![]() CD,
CD,
∴PQ![]() P′Q′,
P′Q′,
∴P′Q′PQ是平行四边形,
∴Q′,Q关于点B对称,
∴Q′![]() ,
,
③ 当CD为对角线时,四边形DPCQ′′为平行四边形,
同①,由平移可得Q′′![]() ,
,
∴Q的坐标为![]()
![]() 或
或![]()
-
科目: 来源: 题型:
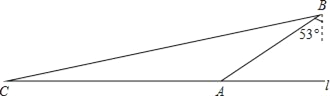
查看答案和解析>>【题目】如图,在自动向西的公路l上有一检查站A,在观测点B的南偏西53°方向,检查站一工作人员家住在与观测点B的距离为7
 km,位于点B南偏西76°方向的点C处,求工作人员家到检查站的距离AC.(参考数据:sin76°≈
km,位于点B南偏西76°方向的点C处,求工作人员家到检查站的距离AC.(参考数据:sin76°≈ ,cos76°≈
,cos76°≈ ,tan 76°≈4,sin53°≈
,tan 76°≈4,sin53°≈ ,tan53°≈
,tan53°≈ )
)
-
科目: 来源: 题型:
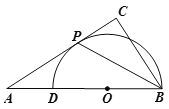
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AC相切于点P.
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
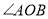 是平角,
是平角,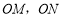 分别是
分别是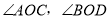 的平分线.
的平分线.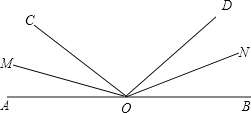
(1)已知
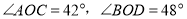 ,求
,求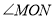 的度数;
的度数;(2)如果(1)中的已知“
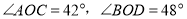 ”,改为已知“
”,改为已知“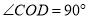 ”,你能求出
”,你能求出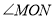 的度数吗?如果能,请求出;如果不能,请说明理由.
的度数吗?如果能,请求出;如果不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(定义学习)
定义:如果四边形有一组对角为直角,那么我们称这样的四边形为“对直四边形”
(判断尝试)
在①梯形;②矩形:③菱形中,是“对直四边形”的是哪一个. (填序号)
(操作探究)
在菱形ABCD中,
 于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,
于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,
(实践应用)
某加工厂有一批四边形板材,形状如图所示,若AB=3米,AD=1米,


.现根据客户要求,需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形"板材,且这两个等腰三角形的腰长相等,要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长,

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题一:如图1,已知A,C两点之间的距离为16 cm,甲,乙两点分别从相距3cm的A,B两点同时出发到C点,若甲的速度为8 cm/s,乙的速度为6 cm/s,设乙运动时间为x(s), 甲乙两点之间距离为y(cm).
(1)当甲追上乙时,x = .
(2)请用含x的代数式表示y.
当甲追上乙前,y= ;
当甲追上乙后,甲到达C之前,y= ;
当甲到达C之后,乙到达C之前,y= .

问题二:如图2,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.
(1)分针OD指向圆周上的点的速度为每分钟转动 cm;时针OE指向圆周上的点的速度为每分钟转动 cm.
(2)若从4:00起计时,求几分钟后分针与时针第一次重合.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列的解题过程,然后回答下列问题.
例:解绝对值方程:
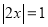 .
.解:讨论:①当
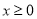 时,原方程可化为
时,原方程可化为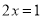 ,它的解是
,它的解是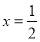 ;
;②当
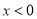 时,原方程可化为
时,原方程可化为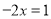 ,它的解是
,它的解是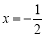 .
.原方程的解为
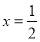 或
或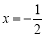 .
.(1)依例题的解法,方程算
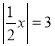 的解是_______;
的解是_______;(2)尝试解绝对值方程:
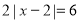 ;
;(3)在理解绝对值方程解法的基础上,解方程:
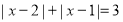 .
.
相关试题

