【题目】问题一:如图1,已知A,C两点之间的距离为16 cm,甲,乙两点分别从相距3cm的A,B两点同时出发到C点,若甲的速度为8 cm/s,乙的速度为6 cm/s,设乙运动时间为x(s), 甲乙两点之间距离为y(cm).
(1)当甲追上乙时,x = .
(2)请用含x的代数式表示y.
当甲追上乙前,y= ;
当甲追上乙后,甲到达C之前,y= ;
当甲到达C之后,乙到达C之前,y= .
![]()
问题二:如图2,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.
(1)分针OD指向圆周上的点的速度为每分钟转动 cm;时针OE指向圆周上的点的速度为每分钟转动 cm.
(2)若从4:00起计时,求几分钟后分针与时针第一次重合.

参考答案:
【答案】问题一、(1)![]() ;(2)3-2x;2x-3;13-6x;问题一、(1)
;(2)3-2x;2x-3;13-6x;问题一、(1)![]() ;
;![]() ;
;![]() .
.
【解析】
问题一根据等量关系,路程=速度![]() 时间,路程差=路程1-路程2,即可列出方程求解。
时间,路程差=路程1-路程2,即可列出方程求解。
问题一:(1)当甲追上乙时,甲的路程=乙的路程+3
所以,![]()
![]()
![]()
故答案为![]() .
.
(2) 当甲追上乙前,路程差=乙所行的路程+3-甲所行的路程;
所以,![]() .
.
当甲追上乙后,甲到达C之前,路程差=甲所行的路程-3-乙所行的路程;
所以,![]() .
.
当甲到达C之后,乙到达C之前,路程差=总路程-3-乙所行的路程;
所以,![]() .
.
问题二:(1)由题意AB为钟表外围的一部分,且∠AOB=30°
可知,钟表外围的长度为![]()
分针OD的速度为![]()
时针OE的速度为![]()
故OD每分钟转动![]() ,OE每分钟转动
,OE每分钟转动![]() .
.
(2)4点时时针与分针的路程差为![]()
设![]() 分钟后分针与时针第一次重合。
分钟后分针与时针第一次重合。
由题意得,![]()
解得,![]() .
.
即![]() 分钟后分针与时针第一次重合。
分钟后分针与时针第一次重合。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示数a,点C表示数c,且
 .我们把数轴上两点之间的距离用表示两点的大写字母一起标记.
.我们把数轴上两点之间的距离用表示两点的大写字母一起标记.
比如,点A与点B之间的距离记作AB.
(1)求AC的值;
(2)若数轴上有一动点D满足CD+AD=36,直接写出D点表示的数;
(3)动点B从数1对应的点开始向右运动,速度为每秒1个单位长度,同时点A,C在数轴上运动,点A、C的速度分别为每秒 3个单位长度,每秒4个单位长度,运动时间为t秒.
①若点A向右运动,点C向左运动,AB=BC,求t的值.
②若点A向左运动,点C向右运动,2AB-m×BC的值不随时间t的变化而改变,请求出m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,以下几种说法中:①
 和
和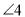 是同位角;②
是同位角;② 和
和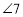 是同位角;③
是同位角;③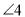 和
和 是内错角;④
是内错角;④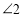 和
和 是同旁内角;⑤
是同旁内角;⑤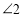 和
和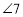 是同位角;⑥
是同位角;⑥ 和
和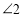 是同位角;正确的个数是( )
是同位角;正确的个数是( )
A.3B.4C.5D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=12,AB=10,则AE的长为( )

A. 16B. 15C. 14D. 13
-
科目: 来源: 题型:
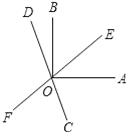
查看答案和解析>>【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简再求值:
 ,其中a、b满足
,其中a、b满足
(2)已知a+b=4,ab=-2,求代数式(5a-4b-4ab)-3(a-2b-ab)的值.
-
科目: 来源: 题型:
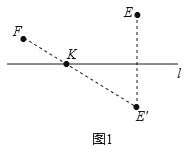
查看答案和解析>>【题目】如图1,点EF在直线l的同一侧,要在直线l上找一点K,使KE与KF的距离之和最小,我们可以作出点E关于l的对称点E′,连接FE′交直线L于点K,则点K即为所求.
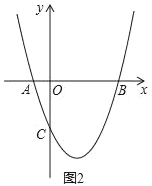
(1)(实践运用)抛物线y=ax2+bx+c经过点A(﹣1,0)、B(3,0)、C(0,﹣3).如图2.
①求该抛物线的解析式;
②在抛物线的对称轴上找一点P,使PA+PC的值最小,并求出此时点P的坐标及PA+PC的最小值.
(2)(知识拓展)在对称轴上找一点Q,使|QA﹣QC|的值最大,并求出此时点Q的坐标.
相关试题

