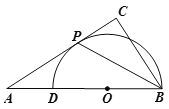
【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AC相切于点P.
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接OP,首先证明OP∥BC,推出∠OPB=∠PBC,由OP=OB,推出∠OPB=∠OBP,由此推出∠PBC=∠OBP;
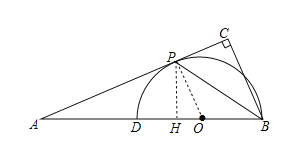
(2)作PH⊥AB于H.首先证明PC=PH=1,在Rt△APH中,求出AH,由△APH∽△ABC,求出AB、BH,由Rt△PBC≌Rt△PBH,推出BC=BH即可解决问题.
试题解析:
(1)连接OP,
∵AC是⊙O的切线,
∴OP⊥AC,
∴∠APO=∠ACB=90°,
∴OP∥BC,
∴∠OPB=∠PBC,
∵OP=OB,
∴∠OPB=∠OBP,
∴∠PBC=∠OBP,
∴BP平分∠ABC;
(2)作PH⊥AB于H.则∠AHP=∠BHP=∠ACB=90°,
又∵∠PBC=∠OBP,PB=PB,
∴△PBC≌△PBH ,
∴PC=PH=1,BC=BH,
在Rt△APH中,AH=![]() ,
,
在Rt△ACB中,AC2+BC2=AB2
∴(AP+PC)2+BC2=(AH+HB)2,
即42+BC2=(![]() +BC)2,
+BC)2,
解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:
(1)探究:
①数轴上表示
 和
和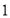 的两点之间的距离是 ;
的两点之间的距离是 ;②数轴上表示
 和
和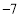 的两点之间的距离是 ;
的两点之间的距离是 ;③数轴上表示
 和
和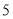 的两点之间的距离是 ;
的两点之间的距离是 ;(2)归纳:
一般的,数轴上表示数m与数n的两点之间的距离等于 .
(3)应用:
①如果表示数
 和3的两点之间的距离是9,则可记为:
和3的两点之间的距离是9,则可记为: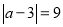 ,那么
,那么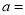 .
.②若数轴上表示数
 的点位于
的点位于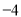 与
与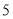 之间,求
之间,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列说法:
①2+3x-5x3是三次四项式;②﹣a一定在原点的左边.③
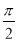 是分数,它是有理数;④有最大的负整数,没有最大的正整数;⑤近似数5.60所表示的准确数x的范围是:5.55≤x<5.65.其中错误的个数是( )
是分数,它是有理数;④有最大的负整数,没有最大的正整数;⑤近似数5.60所表示的准确数x的范围是:5.55≤x<5.65.其中错误的个数是( )A.2B.3C.4D.5
-
科目: 来源: 题型:
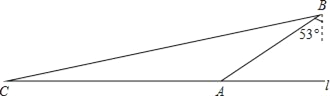
查看答案和解析>>【题目】如图,在自动向西的公路l上有一检查站A,在观测点B的南偏西53°方向,检查站一工作人员家住在与观测点B的距离为7
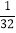 km,位于点B南偏西76°方向的点C处,求工作人员家到检查站的距离AC.(参考数据:sin76°≈
km,位于点B南偏西76°方向的点C处,求工作人员家到检查站的距离AC.(参考数据:sin76°≈ ,cos76°≈
,cos76°≈ ,tan 76°≈4,sin53°≈
,tan 76°≈4,sin53°≈ ,tan53°≈
,tan53°≈ )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
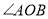 是平角,
是平角,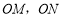 分别是
分别是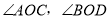 的平分线.
的平分线.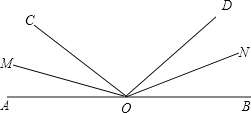
(1)已知
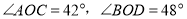 ,求
,求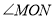 的度数;
的度数;(2)如果(1)中的已知“
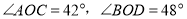 ”,改为已知“
”,改为已知“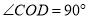 ”,你能求出
”,你能求出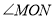 的度数吗?如果能,请求出;如果不能,请说明理由.
的度数吗?如果能,请求出;如果不能,请说明理由. -
科目: 来源: 题型:
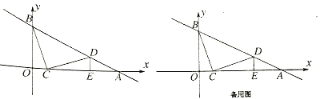
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线 y=kx+b与x 轴、y 轴相交干A(6,0),B(0,3)两点,动点C在线段OA上,将线段CB 绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D 作DE⊥x 轴于点E
(1)求直线y=kx+b 的表达式及点D 的坐标;
(2)若点P在y 轴上,点Q在直线AB上,是否存在以C、D、P、Q 为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q 点坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(定义学习)
定义:如果四边形有一组对角为直角,那么我们称这样的四边形为“对直四边形”
(判断尝试)
在①梯形;②矩形:③菱形中,是“对直四边形”的是哪一个. (填序号)
(操作探究)
在菱形ABCD中,
 于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,
于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,
(实践应用)
某加工厂有一批四边形板材,形状如图所示,若AB=3米,AD=1米,


.现根据客户要求,需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形"板材,且这两个等腰三角形的腰长相等,要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长,

相关试题

