搜索
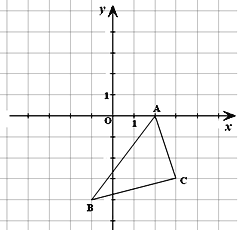
【题目】如图所示的直角坐标系中，解答下列问题：
（1）分别写出A、B两点的坐标；
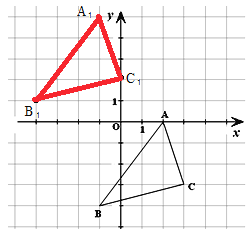
（2）将△ABC向左平移3个单位长度，再向上平移5个单位长度，画出平移后的△A1B1C1；
（3）求 △A1B1C1的面积。
参考答案：
【答案】（1）A（2,0） B（-1,-4）；（2）作图见解析；（3）
【解析】试题分析：（1）从直角坐标系中读出点的坐标．
（2）根据平移规律找出各点平移后后得到对应点，顺次连接即可．
（3）根据S△ABC=S长方形ADEF-S△ABD-S△EBC-S△ACF，即可求得三角形的面积．
试题解析：（1）A（2,0） B（-1,-4）
（2）如图，
（3）如图，
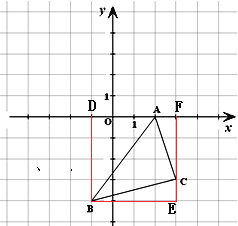
S△ABC=S长方形DBEF-S△ABD-S△EBC-S△ACF
=4×4-
×4×1-
×3×1-
×4×3=
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学积极组织学生开展课外阅读活动，为了解本校学生每周课外阅读的时间量t（单位：小时），采用随机抽样的方法抽取部分学生进行了问卷调查，调查结果按0≤t＜2，2≤t＜3，3≤t＜4，t≥4分为四个等级，并分别用A、B、C、D表示，根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图，由图中给出的信息解答下列问题：
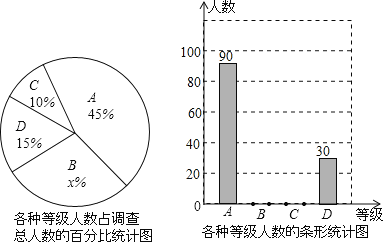
（1）求出x的值和抽取的学生人数;
（2）将不完整的条形统计图补充完整；
（3）若该校共有学生2500人，试估计每周课外阅读时间量满足2≤t＜4的人数.
-
科目： 来源： 题型：
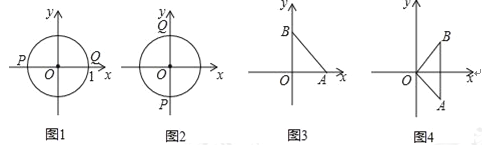
查看答案和解析>>【题目】在平面直角坐标系xOy中，设点P（x1，y1），Q（x2，y2）是图形W上的任意两点．
定义图形W的测度面积：若|x1﹣x2|的最大值为m，|y1﹣y2|的最大值为n，则S=mn为图形W的测度面积．
例如，若图形W是半径为1的⊙O，当P，Q分别是⊙O与x轴的交点时，如图1，|x1﹣x2|取得最大值，且最大值m=2；当P，Q分别是⊙O与y轴的交点时，如图2，|y1﹣y2|取得最大值，且最大值n=2．则图形W的测度面积S=mn=4
（1）若图形W是等腰直角三角形ABO，OA=OB=1．
①如图3，当点A，B在坐标轴上时，它的测度面积S= ；
②如图4，当AB⊥x轴时，它的测度面积S= ；
（2）若图形W是一个边长1的正方形ABCD，则此图形的测度面积S的最大值为 ；
（3）若图形W是一个边长分别为3和4的矩形ABCD，求它的测度面积S的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，BC交⊙O于点D，E是
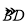的中点，连接AE交BC于点F，∠ACB=2∠EAB．
（1）求证：AC是⊙O的切线；
（2）若cosC=
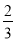，AC=6，求BF的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】某中学准备随机选出七、八、九三个年级各1名学生担任学校国旗升旗手．现已知这三个年级每个年级分别选送一男、一女共6名学生作为备选人．
（1）请你利用树状图或表格列出所有可能的选法；
（2）求选出“一男两女”三名国旗升旗手的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一个四边形花坛ABCD，被两条线段MN,EF分成四个部分，分别种上红、黄、紫、白四种花卉，种植面积依次是S1,S2,S3,S4，若MN∥AB∥CD，EF∥DA∥CB，则有（ ）
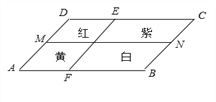
A. S1=S4 B. S1+S4=S2+S3 C. S1S4=S2S3 D. 都不对
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列现象中，可用基本事实“两点之间，线段最短”来解释的现象是（ ）
A. 用两个钉子就可以把木条固定在墙上
B. 把弯曲的公路改直，就能缩短路程
C. 利用圆规可以比较两条线段的大小关系
D. 植树时，只要定出两棵树的位置，就能确定同一行树所在的直线。
相关试题
