【题目】在平面直角坐标系xOy中,设点P(x1,y1),Q(x2,y2)是图形W上的任意两点.
定义图形W的测度面积:若|x1﹣x2|的最大值为m,|y1﹣y2|的最大值为n,则S=mn为图形W的测度面积.
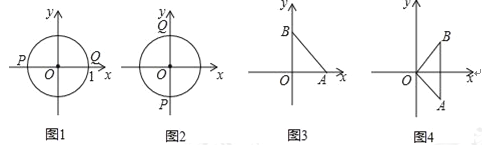
例如,若图形W是半径为1的⊙O,当P,Q分别是⊙O与x轴的交点时,如图1,|x1﹣x2|取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,|y1﹣y2|取得最大值,且最大值n=2.则图形W的测度面积S=mn=4
(1)若图形W是等腰直角三角形ABO,OA=OB=1.
①如图3,当点A,B在坐标轴上时,它的测度面积S= ;
②如图4,当AB⊥x轴时,它的测度面积S= ;
(2)若图形W是一个边长1的正方形ABCD,则此图形的测度面积S的最大值为 ;
(3)若图形W是一个边长分别为3和4的矩形ABCD,求它的测度面积S的取值范围.
参考答案:
【答案】(1)1,1;(2)2;(3)12≤S≤![]() .
.
【解析】
试题分析:(1)由测度面积的定义利用它的测度面积S=|OA||OB|求解即可;
②利用等腰直角三角形的性质求出AC,AB,利用测度面积S=|AB||OC|求解即可;
(2)先确定正方形有最大测度面积S时的图形,即可利用测度面积S=|AC||BD|求解.
(3)分两种情况当A,B或B,C都在x轴上时,当顶点A,C都不在x轴上时分别求解即可.
试题解析:(1)①如图3,
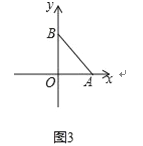
∵OA=OB=1,点A,B在坐标轴上,
∴它的测度面积S=|OA||OB|=1,
故答案为:1.
②如图4,
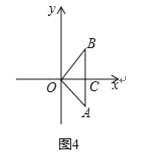
∵AB⊥x轴,OA=OB=1.
∴AB=![]() ,OC=
,OC=![]() ,
,
∴它的测度面积S=|AB||OC|=![]() ×
×![]() =1,
=1,
故答案为:1.
(2)如图5,图形的测度面积S的值最大,
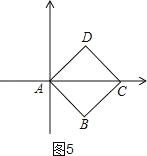
∵四边形ABCD是边长为1的正方形.
∴它的测度面积S=|AC||BD|=![]() ×
×![]() =2,
=2,
故答案为:2.
(3)设矩形ABCD的边AB=4,BC=3,由已知可得,平移图形W不会改变其测度面积的大小,将矩形ABCD的其中一个顶点B平移至x轴上,
当A,B或B,C都在x轴上时,
如图6,图7,
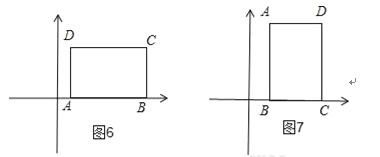
矩形ABCD的测度面积S就是矩形ABCD的面积,此时S=12.
当顶点A,C都不在x轴上时,如图8,过点A作直线AH⊥x轴于点E,过C点作CF⊥x轴于点F,过点D作直线GH∥x轴,分别交AE,CF于点H,G,则可得四边形EFGH是矩形,
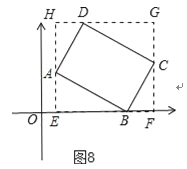
当点P,Q与点A,C重合时,|x1﹣x2|的最大值为m=EF,|y1﹣y2|的最大值为n=GF.
图形W的测度面积S=EFGF,
∵∠ABC+∠CBF=90°,∠ABC+∠BAE=90°,
∴∠CBF=∠BAE,
∵∠AEB=∠BFC=90°,
∴△AEB∽△BFC,
∴![]() ,
,
设AE=4a,EB=4b,(a>0,b>0),则BF=3a,FC=3b,
在RT△AEB中,AE2+BE2=AB2,
∴16a2+16b2=16,即a2+b2=1,
∵b>0,
∴![]() ,
,
在△ABE和△CDG中,
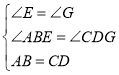
∴△ABE≌△CDG(AAS)
∴CG=AE=4a,
∴EF=EB+BF=4b+3a,GF=FC+CG=3b+4a,
∴图形W的测度面积S=EFGF=(4b+3a)(3b+4a)
=12a2+12b2+25a![]() =12+25
=12+25![]() =12+25
=12+25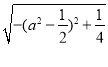 ,
,
当![]() 时,即a=
时,即a=![]() 时,测度面积S取得最大值12+25×
时,测度面积S取得最大值12+25×![]() =
=![]() ,
,
∵a>0,b>0,
∴![]() ,
,
∴S>12,
综上所述:测度面积S的取值范围为12≤S≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多边形内角和是外角和的4倍,则这个多边形是( )
A. 八边形B. 九边形C. 十边形D. 十二边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市需调查该市九年级男生的体能状况,为此抽取了50名九年级男生进行引体向上个数测试,测试情况绘制成表格如下:
个数
1
2
3
4
5
6
7
8
9
10
11
人数
1
1
6
18
10
6
2
2
1
1
2
(1)求这次抽样测试数据的平均数、众数和中位数;
(2)在平均数、众数和中位数中,你认为用哪一个统计量作为该市九年级男生引体向上项目测试的合格标准个数较为合适?简要说明理由;
(3)如果该市今年有3万名九年级男生,根据(2)中你认为合格的标准,试估计该市九年级男生引体向上项目测试的合格人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
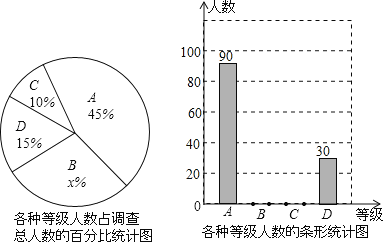
(1)求出x的值和抽取的学生人数;
(2)将不完整的条形统计图补充完整;
(3)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t<4的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是
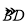 的中点,连接AE交BC于点F,∠ACB=2∠EAB.
的中点,连接AE交BC于点F,∠ACB=2∠EAB.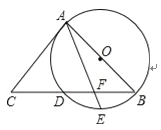
(1)求证:AC是⊙O的切线;
(2)若cosC=
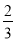 ,AC=6,求BF的长.
,AC=6,求BF的长. -
科目: 来源: 题型:
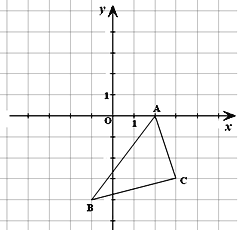
查看答案和解析>>【题目】如图所示的直角坐标系中,解答下列问题:
(1)分别写出A、B两点的坐标;
(2)将△ABC向左平移3个单位长度,再向上平移5个单位长度,画出平移后的△A1B1C1;
(3)求 △A1B1C1的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学准备随机选出七、八、九三个年级各1名学生担任学校国旗升旗手.现已知这三个年级每个年级分别选送一男、一女共6名学生作为备选人.
(1)请你利用树状图或表格列出所有可能的选法;
(2)求选出“一男两女”三名国旗升旗手的概率.
相关试题

