【题目】如图,一个四边形花坛ABCD,被两条线段MN,EF分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S1,S2,S3,S4,若MN∥AB∥CD,EF∥DA∥CB,则有( )
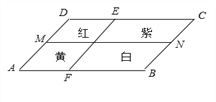
A. S1=S4 B. S1+S4=S2+S3 C. S1S4=S2S3 D. 都不对
参考答案:
【答案】C
【解析】设红、紫四边形的高相等为h1,黄、白四边形的高相等,高为h2,
则S1=DEh1,S2=AFh2,S3=ECh1,S4=FBh2,
因为DE=AF,EC=FB,所以A不对;
S1+S4=DEh1+FBh2=AFh1+FBh2,
S2+S3=AFh2+ECh1=AFh2+FBh1,
所以B不对;
S1S4=DEh1FBh2=AFh1FBh2,
S2S3=AFh2ECh1=AFh2FBh1,
所以S1S4=S2S3,
故选C。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是
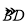 的中点,连接AE交BC于点F,∠ACB=2∠EAB.
的中点,连接AE交BC于点F,∠ACB=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)若cosC=
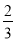 ,AC=6,求BF的长.
,AC=6,求BF的长. -
科目: 来源: 题型:
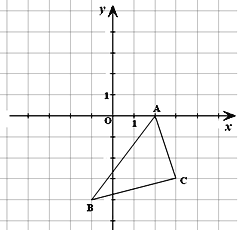
查看答案和解析>>【题目】如图所示的直角坐标系中,解答下列问题:
(1)分别写出A、B两点的坐标;
(2)将△ABC向左平移3个单位长度,再向上平移5个单位长度,画出平移后的△A1B1C1;
(3)求 △A1B1C1的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学准备随机选出七、八、九三个年级各1名学生担任学校国旗升旗手.现已知这三个年级每个年级分别选送一男、一女共6名学生作为备选人.
(1)请你利用树状图或表格列出所有可能的选法;
(2)求选出“一男两女”三名国旗升旗手的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列现象中,可用基本事实“两点之间,线段最短”来解释的现象是( )
A. 用两个钉子就可以把木条固定在墙上
B. 把弯曲的公路改直,就能缩短路程
C. 利用圆规可以比较两条线段的大小关系
D. 植树时,只要定出两棵树的位置,就能确定同一行树所在的直线。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a4+a4=a 8
B.(a3)4=a7
C.12a6b4÷3a2b-2=4a4b2
D.(-a3b)2=a6b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(3,-4),点B的坐标是(1,2),将线段AB平移后得到线段A'B'.若点A对应点A'的坐标是(5,2),则点B'的坐标是( )
A. (3,6)B. (3,7)C. (3,8)D. (6,4)
相关试题

