【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,
,![]() ,
,![]() .
.
(1)在所给坐标系中作出![]() 关于y轴的对称图形
关于y轴的对称图形![]() ;
;
(2)分别写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 的周长最小,若存在,在所给坐标系中作出点
的周长最小,若存在,在所给坐标系中作出点![]() (不写作法,保留作图痕迹)并写出点
(不写作法,保留作图痕迹)并写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

参考答案:
【答案】(1)见解析;(2)A1(1,4),B1(2,0), C1(4,2).(3)P(-3,0)
【解析】
(1)分别作出三个顶点关于y轴的对称点,再首尾顺次连接可得;
(2)根据直角坐标系即可依次写出;
(3)如图所示,作点C关于x轴的对称点C,连接AC 交x轴于点P,点P为所求,再根据直角坐标系得到坐标.
(1)解:如图所示;
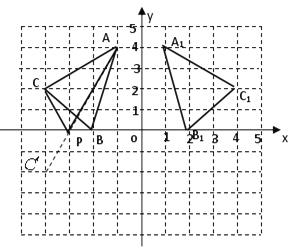
(2)由坐标系可得A1(1,4),B1(2,0), C1(4,2).
(3)解:如图所示,作点C关于x轴的对称点C,连接AC 交x轴于点P,点P为所求.故 P点坐标为(-3,0).
-
科目: 来源: 题型:
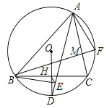
查看答案和解析>>【题目】如图,
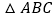 内接于
内接于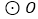 ,
, 是弧
是弧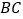 的中点,
的中点, 交
交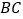 于点
于点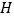 ,且
,且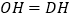 ,连接
,连接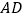 ,过点
,过点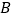 作
作 于点
于点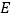 ,连接
,连接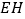 ,
, 于
于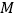 ,若
,若 ,
,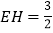 ,则
,则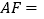 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
 ,其中
,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

-
科目: 来源: 题型:
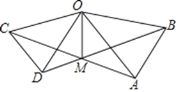
查看答案和解析>>【题目】如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的是____________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
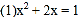
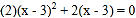
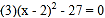
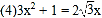 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
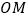 、
、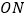 为相交成
为相交成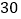 度角的两条公路,在
度角的两条公路,在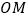 上距
上距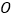 点
点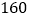 米有一所小学
米有一所小学 ,拖拉机沿
,拖拉机沿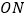 方向以每小时
方向以每小时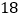 千米的速度行驶,在小学周围
千米的速度行驶,在小学周围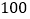 米范围内会受到拖拉机噪音的影响.试问小学是否会受到拖拉机噪音的影响?若受到影响,影响时间有多长?
米范围内会受到拖拉机噪音的影响.试问小学是否会受到拖拉机噪音的影响?若受到影响,影响时间有多长?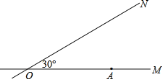
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
相关试题

