【题目】解方程:
![]()
![]()
![]()
![]() .
.
参考答案:
【答案】![]()
![]() ;(3)x1=
;(3)x1=![]() ,x2=
,x2=![]() ;(4)
;(4)![]() .
.
【解析】
(1)方程整理为一般形式,找出a,b,c的值,代入求根公式即可求出解.
(2)方程利用因式分解法求出解即可.
(3)利用开平方的定义解方程.
(4)方程移项,则左边是完全平方式,右边是常数,再利用直接开平方法即可求解.
(1)方程整理得:x2+2x﹣1=0,这里a=1,b=2,c=﹣1.
∵△=4+4=8,∴x=![]() ,∴x1=
,∴x1=![]() ,x2=
,x2=![]() ;
;
(2)分解因式得:(x﹣3)(x﹣3+2)=0,可得x﹣3=0或x﹣1=0,解得:x1=3,x2=1.
(3)移项得:(x﹣2)2=27
开平方得:x﹣2=±3![]()
移项得:x1=![]() ,x2=
,x2=![]() .
.
(4)∵3x2+1=2![]() x,∴3x2﹣2
x,∴3x2﹣2![]() x+1=0,∴(
x+1=0,∴(![]() x﹣1)2=0,∴x1=x2=
x﹣1)2=0,∴x1=x2=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
 ,其中
,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

-
科目: 来源: 题型:
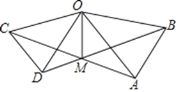
查看答案和解析>>【题目】如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的是____________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,点
中,点 ,
, ,
, .
.(1)在所给坐标系中作出
 关于y轴的对称图形
关于y轴的对称图形 ;
;(2)分别写出点
 ,
, ,
, 的坐标;
的坐标;(3)在
 轴上是否存在一点
轴上是否存在一点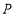 ,使
,使 的周长最小,若存在,在所给坐标系中作出点
的周长最小,若存在,在所给坐标系中作出点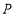 (不写作法,保留作图痕迹)并写出点
(不写作法,保留作图痕迹)并写出点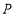 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 、
、 为相交成
为相交成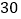 度角的两条公路,在
度角的两条公路,在 上距
上距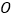 点
点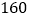 米有一所小学
米有一所小学 ,拖拉机沿
,拖拉机沿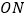 方向以每小时
方向以每小时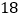 千米的速度行驶,在小学周围
千米的速度行驶,在小学周围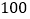 米范围内会受到拖拉机噪音的影响.试问小学是否会受到拖拉机噪音的影响?若受到影响,影响时间有多长?
米范围内会受到拖拉机噪音的影响.试问小学是否会受到拖拉机噪音的影响?若受到影响,影响时间有多长?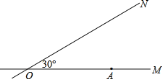
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年圣诞节前夕,小明、小丽两位同学到某超市调研一种袜子的销售情况,
这种袜子的进价为每双 1 元,请根据小丽提供的信息解决小明提出的问题.
小丽:每双定价 2 元,每天能卖出 500 双,而且这种袜子的售价每上涨 0.1 元,其每天的销售量将减少 10 双.
小明:照你所说,如果要实现每天 800 元的销售利润,那该如何定价?别忘了,物价局有规定,售价不能超过进价的 300%呦.
相关试题

