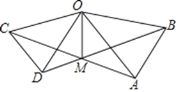
【题目】如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的是____________________________
参考答案:
【答案】①②④
【解析】
由SAS证明△AOC≌△BOD得出∠OCA=∠ODB,AC=BD,①正确;
由全等三角形的性质得出∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,得出∠AMB=∠AOB=40°,②正确;
作OG⊥MC于G,OH⊥MB于H,如图2所示:则∠OGC=∠OHD=90°,由AAS证明△OCG≌△ODH(AAS),得出OG=OH,由角平分线的判定方法得出MO平分∠BMC,④正确;
由∠AOB=∠COD,得出当∠DOM=∠AOM时,OM才平分∠BOC,假设∠DOM=∠AOM,由△AOC≌△BOD得出∠COM=∠BOM,由MO平分∠BMC得出∠CMO=∠BMO,推出△COM≌△BOM,得OB=OC,而OA=OB,所以OA=OC,而OA>OC,故③错误;即可得出结论.
解:∵∠AOB=∠COD=40°,
∴∠AOB+∠AOD=∠COD+∠AOD,
即∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,AC=BD,①正确;
∴∠OAC=∠OBD,
由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,
∴∠AMB=∠AOB=40°,②正确;
作OG⊥MC于G,OH⊥MB于H,如图2所示:

则∠OGC=∠OHD=90°,
在△OCG和△ODH中,
∴△OCG≌△ODH(AAS),
∴OG=OH,
∴MO平分∠BMC,④正确;
∵∠AOB=∠COD,
∴当∠DOM=∠AOM时,OM才平分∠BOC,
假设∠DOM=∠AOM
∵△AOC≌△BOD,
∴∠COM=∠BOM,
∵MO平分∠BMC,
∴∠CMO=∠BMO,
在△COM和△BOM中,
∴△COM≌△BOM(ASA),
∴OB=OC,
∵OA=OB
∴OA=OC
与OA>OC矛盾,
∴③错误;
正确的是①②④;
故答案为:①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4, △ABC的面积是( )
的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4, △ABC的面积是( )
A.21B.42C.56D.84
-
科目: 来源: 题型:
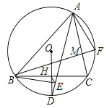
查看答案和解析>>【题目】如图,
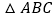 内接于
内接于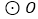 ,
, 是弧
是弧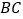 的中点,
的中点, 交
交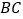 于点
于点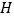 ,且
,且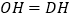 ,连接
,连接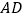 ,过点
,过点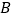 作
作 于点
于点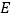 ,连接
,连接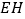 ,
, 于
于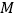 ,若
,若 ,
,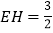 ,则
,则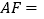 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
 ,其中
,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,点
中,点 ,
, ,
, .
.(1)在所给坐标系中作出
 关于y轴的对称图形
关于y轴的对称图形 ;
;(2)分别写出点
 ,
, ,
, 的坐标;
的坐标;(3)在
 轴上是否存在一点
轴上是否存在一点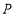 ,使
,使 的周长最小,若存在,在所给坐标系中作出点
的周长最小,若存在,在所给坐标系中作出点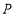 (不写作法,保留作图痕迹)并写出点
(不写作法,保留作图痕迹)并写出点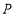 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
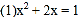
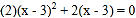
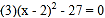
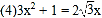 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
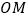 、
、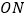 为相交成
为相交成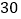 度角的两条公路,在
度角的两条公路,在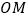 上距
上距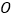 点
点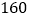 米有一所小学
米有一所小学 ,拖拉机沿
,拖拉机沿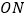 方向以每小时
方向以每小时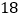 千米的速度行驶,在小学周围
千米的速度行驶,在小学周围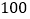 米范围内会受到拖拉机噪音的影响.试问小学是否会受到拖拉机噪音的影响?若受到影响,影响时间有多长?
米范围内会受到拖拉机噪音的影响.试问小学是否会受到拖拉机噪音的影响?若受到影响,影响时间有多长?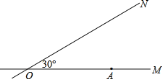
相关试题

