搜索
【题目】如图，直线y=﹣
x+8与x轴，y轴分别交于点A和B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处，则直线AM的解析式为 ．
参考答案：
【答案】y=-0.5x+3
【解析】此题首先分别求出A，B两个点的坐标，得到OA，OB的长度，再根据勾股定理求出AB，再求出OB′，然后根据已知得到BM=B′M，设BM=x，在Rt△B′OM中利用勾股定理求出x，这样可以求出OM，从而求出了M的坐标，最后用待定系数法求直线的解析式．
解：当x=0时，y=8；当y=0时，x=6，
∴OA=6，OB=8，
∴AB=10，
根据已知得到BM=B'M，
AB'=AB=10，
∴OB'=4，设BM=x，则B'M=x，
OM=8﹣x，在直角△B'MO中，x2=（8﹣x）2+42，
∴x=5，
∴OM=3，
∴M（0，3），
设直线AM的解析式为y=kx+b，把M（0，3），A（6，0）代入其中
得:
∴k=﹣
，b=3，
∴y=﹣x+3．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，函数y=
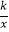（x＞0，k是常数）的图象经过A（2，6），B（m，n），其中m＞2．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，AC与BD交于点E，连结AD，DC，CB．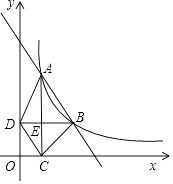
（1）若△ABD的面积为3，求k的值和直线AB的解析式；
（2）求证：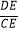
= 
；
（3）若AD∥BC，求点B的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知线段AB=
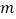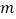(为常数)，点C为直线AB上一点，点P、Q分别在线段BC、AC上，且满足CQ=2AQ，CP=2BP.(1)如图，当点C恰好在线段AB中点时，则PQ=_______(用含
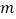的代数式表示)；(2)若点C为直线AB上任一点，则PQ长度是否为常数?若是，请求出这个常数；若不是，请说明理由；
(3)若点C在点A左侧，同时点P在线段AB上(不与端点重合)，请判断2AP+CQ-2PQ与1的大小关系，并说明理由。
-
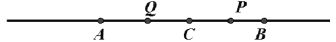
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD，CE⊥CD，且CE=CD，连接BD、DE、BE,则下列结论：①∠ECA=165°，②BE=BC；③AD=BE；④CD=BD．其中正确的是 （ ）
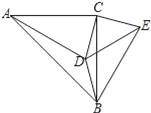
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC边于点D，交AC边于点E．过点D作⊙O的切线，交AC于点F，交AB的延长线于点G，连接DE．
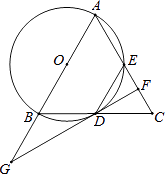
（1）求证：BD=CD；
（2）若∠G=40°，求∠AED的度数．
（3）若BG=6，CF=2，求⊙O的半径． -
科目： 来源： 题型：
查看答案和解析>>【题目】有这样一个问题：
计算代数式
（其中x≠0）的值后填入下表．并根据表格所反映出的（其中x≠0）的值与x之间的变化规律进行探究．x
……
0.25
0.5
1
10
100
1000
10000
……
……
……
下面是小东计算代数式
（其中x≠0）的值后填入表格，并根据表格进行探究的过程，请补充完整：x
……
0.25
0.5
1
10
100
1000
10000
……
……
2
1
……
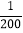
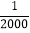
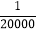
（1）上表是
（其中x≠0）与x的几组对应值．直接写出x＝10时，求代数式的值；（2）随着x值的增大，代数式
的值有何变化（回答“增大”或“减少”）；（3）当x值无限增大时，代数式
的值无限趋近于一个数，这个数是多少． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数y=2x-4
（1）画出函数的图象；
（2）判断点A(1，-2)，B(2，1)是否在该函数的图象上.
（3）已知点A(-2，b)在该函数图像上，求b值；
相关试题
