【题目】如图,![]() 内接于
内接于![]() ,
,![]() 是弧
是弧![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 于
于![]() ,若
,若![]() ,
,![]() ,则
,则![]() ________.
________.
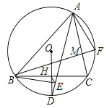
参考答案:
【答案】![]()
【解析】
如图,延长BE交AC的延长线于N,连接OB、OC、BD.首先证明AB=AN,推出AB=8,再证明△OBD是等边三角形,推出∠BAC=60°,利用勾股定理分别求出BM、BC,再利用△AMF∽△BMC,得![]() =
=![]() ,即可解决问题.
,即可解决问题.
如图,延长BE交AC的延长线于N,连接OB、OC、BD.
∵![]() =
=![]() ,∴∠EAB=∠EAN.
,∴∠EAB=∠EAN.
∵AD⊥BN,∴∠AEB=∠AEN=90°,∴∠ABE+∠BAE=90°,∠N+∠EAN=90°,∴∠ABE=∠N,∴AB=AN,∴BE=EN.
∵OD⊥BC,∴BH=HC,∴CN=2EH=3,∴AB=AN=AC+CN=8.
∵OH=HD,BH⊥OD,∴BO=BD=OD,∴∠BOD=∠DOC=60°,∴∠BAC=![]() ∠BOC=60°.
∠BOC=60°.
∵BF⊥AC,∴∠AMB=90°,∴∠ABM=30°.在Rt△AMB中,AM=![]() AB=4,BM=4
AB=4,BM=4![]() .在Rt△BMC中,BC=
.在Rt△BMC中,BC=![]() =
=![]() =7.
=7.
∵∠MAF=∠MBC,∠AMF=∠BMC,∴△AMF∽△BMC,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴AF=
,∴AF=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC是等边三角形,将直角三角板DEF如图放置,其中∠F=30°,让△ABC在直角三角板的边EF上向右平移(点C与点F重合时停止).

(1)如图1,当点B与点E重合时,点A恰好落在直角三角板的斜边DF上,证明:EF=2BC.
(2)在△ABC平移过程中,AB,AC分别与三角板斜边的交点为G、H,如图2,线段EB=AH是否始终成立?如果成立,请证明;如果不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:①长度相等的弧是等弧;②平分弦的直径垂直于弦;③直径是弦;④同弧或等弧所对的圆心角相等;⑤在同圆或等圆中,相等的弦所对弧相等;错误的个数为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4, △ABC的面积是( )
的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4, △ABC的面积是( )
A.21B.42C.56D.84
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
 ,其中
,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

-
科目: 来源: 题型:
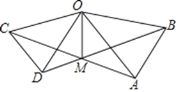
查看答案和解析>>【题目】如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的是____________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,点
中,点 ,
, ,
, .
.(1)在所给坐标系中作出
 关于y轴的对称图形
关于y轴的对称图形 ;
;(2)分别写出点
 ,
, ,
, 的坐标;
的坐标;(3)在
 轴上是否存在一点
轴上是否存在一点 ,使
,使 的周长最小,若存在,在所给坐标系中作出点
的周长最小,若存在,在所给坐标系中作出点 (不写作法,保留作图痕迹)并写出点
(不写作法,保留作图痕迹)并写出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
相关试题

