【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数 ![]() 的图象在第二象限交于点C,CE垂直于x轴,垂足为点E,
的图象在第二象限交于点C,CE垂直于x轴,垂足为点E, ![]() ,OB=4,OE=2.
,OB=4,OE=2.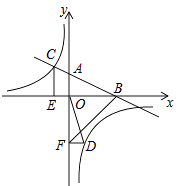
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D做DF垂直于y轴,垂足为点F,连接OD、BF,如果 ![]() ,求点D的坐标.
,求点D的坐标.
参考答案:
【答案】
(1)解:∵OB=4,OE=2,
∴BE=OB+OE=6,
∵CE⊥x轴,
∴∠CEB=90°,
在Rt△BEC中,
∵ ![]() ,
,
∴ ![]() ,即
,即 ![]() ,解得CE=3,
,解得CE=3,
结合图象可知C点的坐标为(-2,3),
将C(-2,3)代入反比例函数解析式可得 ![]() ,解得m=
,解得m= ![]() 6,
6,
∴该反比例函数解析式为 ![]()
(2)解:∵点D在反比例函数 ![]() 第四象限的图象上,
第四象限的图象上,
∴设点D的坐标为(n, ![]() )(n>0).
)(n>0).
在Rt△AOB中,∠AOB=90°,OB=4,tan∠ABO= ![]() ,
,
∴OA=OBtan∠ABO=4× ![]() =2.
=2.
∵S△BAF= ![]() AFOB=
AFOB= ![]() (OA+OF)OB=
(OA+OF)OB= ![]() (2+
(2+ ![]() )×4=4+
)×4=4+ ![]() .
.
∵点D在反比例函数y= ![]() 第四象限的图象上,
第四象限的图象上,
∴S△DFO= ![]() ×|﹣6|=3.
×|﹣6|=3.
∵S△BAF=4S△DFO ,
∴4+ ![]() =4×3,
=4×3,
解得:n= ![]()
经验证,n= ![]() 是分式方程4+
是分式方程4+ ![]() =4×3的解
=4×3的解
∴点D的坐标为( ![]() ,-4)
,-4)
【解析】(1)根据题意求出BE的长,再根据正切的定义求出GE的长,从而得到点C的坐标,再利用待定系数法求出反比例函数的解析式。
(2)根据点D在反比例函数图像上,设出点D的坐标,再根据正切的定义求出OA的长,利用两个三角形的面积关系,得到关于n的方程,求出n的值,进而得到点D的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】请仔细阅读下面材料,然后解决问题:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如:
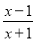 ,
, 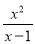 ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: 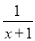 ,
, 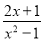 .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如: 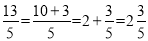 ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:  .
.(1)将分式
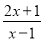 化为带分式;
化为带分式;(2)当x取哪些整数值时,分式
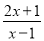 的值也是整数?
的值也是整数?(3)当x的值变化时,分式
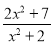 的最大值为 .
的最大值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
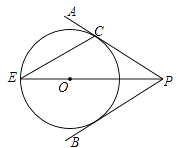
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】填空,完成下列说理过程
如图,点A,O,B在同一条直线上, OD,OE分别平分∠AOC和∠BOC.

(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.
解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD =
 ∠AOC.
∠AOC.因为OE是∠BOC 的平分线,
所以 =
 ∠BOC.
∠BOC.所以∠DOE=∠COD+ =
 (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ∠AOB= °.
∠AOB= °.(2)由(1)可知∠BOE=∠COE = -∠COD= °.
所以∠AOE= -∠BOE = °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点O (0,0),A (-5,0),B (2,1),抛物线
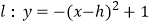 (h为常数)与y轴的交点为C。
(h为常数)与y轴的交点为C。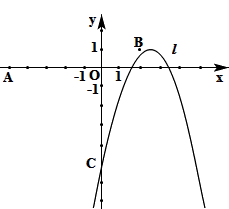
(1)抛物线经过点B,求它的解析式,并写出此时抛物线的对称轴及顶点坐标;
(2)设点C的纵坐标为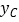 ,求
,求 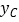 的最大值,此时抛物线上有两点
的最大值,此时抛物线上有两点  ,
,  ,其中
,其中 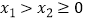 ,比较
,比较 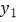 与
与 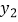 的大小;
的大小;
(3)当线段OA被只分为两部分,且这两部分的比是1:4时,求h的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;

(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家电商场计划用9万元从生产厂家购进50台电视机,已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.
(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你计算一下商场有哪几种进货方案?
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,应选择哪种方案?
相关试题

