【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.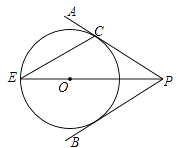
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
参考答案:
【答案】
(1)证明:连接OC,作OD⊥PB于D点.
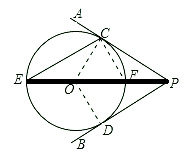
∵⊙O与PA相切于点C, ∴OC⊥PA
(2)解:设PO交⊙O于F,连接CF.
∵OC=3,PC=4,∴PO=5,PE=8.
∵⊙O与PA相切于点C, ∴∠PCF=∠E.
又∵∠CPF=∠EPC, ∴△PCF∽△PEC,
∴CF:CE=PC:PE=4:8=1:2.
∵EF是直径, ∴∠ECF=90°.
设CF=x,则EC=2x.
则x2+(2x)2=62, 解得x= ![]() .
.
则EC=2x= ![]() .
.
【解析】要证明直线PB与⊙O相切,添加辅助线连接OC,作OD⊥PB于D点,再证明OD是圆的半径,根据角平分线上的点到角两边的距离相等及切线的性质,易证得结论。
(2)根据已知易证得△PCF∽△PEC,得出对应边成比例,证出CF:CE=1:2.再根据EF是直径得出△CEF是直角三角形,利用勾股定理求解即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
(2)如果MN=6 cm,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请仔细阅读下面材料,然后解决问题:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如:
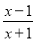 ,
, 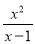 ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: 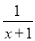 ,
, 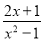 .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如: 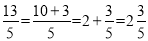 ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:  .
.(1)将分式
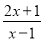 化为带分式;
化为带分式;(2)当x取哪些整数值时,分式
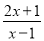 的值也是整数?
的值也是整数?(3)当x的值变化时,分式
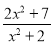 的最大值为 .
的最大值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】填空,完成下列说理过程
如图,点A,O,B在同一条直线上, OD,OE分别平分∠AOC和∠BOC.

(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.
解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD =
 ∠AOC.
∠AOC.因为OE是∠BOC 的平分线,
所以 =
 ∠BOC.
∠BOC.所以∠DOE=∠COD+ =
 (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ∠AOB= °.
∠AOB= °.(2)由(1)可知∠BOE=∠COE = -∠COD= °.
所以∠AOE= -∠BOE = °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数
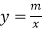 的图象在第二象限交于点C,CE垂直于x轴,垂足为点E,
的图象在第二象限交于点C,CE垂直于x轴,垂足为点E, 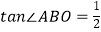 ,OB=4,OE=2.
,OB=4,OE=2.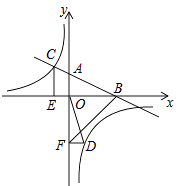
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D做DF垂直于y轴,垂足为点F,连接OD、BF,如果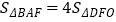 ,求点D的坐标.
,求点D的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点O (0,0),A (-5,0),B (2,1),抛物线
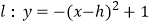 (h为常数)与y轴的交点为C。
(h为常数)与y轴的交点为C。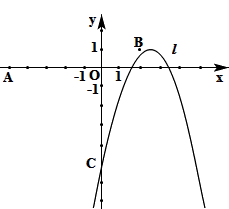
(1)抛物线经过点B,求它的解析式,并写出此时抛物线的对称轴及顶点坐标;
(2)设点C的纵坐标为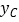 ,求
,求 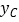 的最大值,此时抛物线上有两点
的最大值,此时抛物线上有两点  ,
,  ,其中
,其中 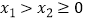 ,比较
,比较 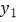 与
与 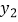 的大小;
的大小;
(3)当线段OA被只分为两部分,且这两部分的比是1:4时,求h的值。
相关试题

