【题目】如图,在边长为5的正方形ABCD中,以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形的个数为( )

A.3B.4C.5D.6
参考答案:
【答案】C
【解析】
分别以3为底和以3为腰构造等腰三角形即可.注意等腰三角形的大小不同.
①以A为圆心,以3为半径作弧,交AD、AB两点,连接即可,此时三角形为腰为3的等腰三角形;
②连接AC,在AC上,以A为端点,截取1.5个单位,过这个点作AC的垂线,交AD、AB两点,连接即可
理由如下:∵四边形ABCD为正方形,
∴∠BAC=∠DAC=45°,
∵EF⊥AC
∴△AEH与△AHF为等腰直角三角形
∴EF=EH+FH=AH+AH=3.且AE=AF=![]()
故△AEF为底为3的等腰三角形;
③以A为端点在AB上截取3个单位,以截取的点为圆心,以3个单位为半径画弧,交BC一个点,连接即可,此时三角形为腰为3的等腰三角形;
④连接AC,在AC上,以C为端点,截取1.5个单位,过这个点作AC的垂线,交BC、DC两点,然后连接A与这两个点即可;
理由如下:与②同理可证EF=3,且EC=FC,
在△DEC和△DFC中,
∵AC=AC,∠ACE=∠ACF,EC=FC
∴△DEC≌△DFC
∴AE=AF,
故△AEF为底为3的等腰三角形.
⑤以A为端点在AB上截取3个单位,再作着个线段的垂直平分线交CD一点,连接即可根据垂直平分线上的点到线段两端距离相等,三角形为底为3的等腰三角形.
故满足条件的所有图形如图所示:
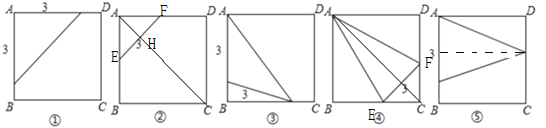
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,函数
 的图象与一次函数y=kx-k的图象的交点为A(m,2).
的图象与一次函数y=kx-k的图象的交点为A(m,2).(1)求一次函数的解析式;
(2)设一次函数y=kx-k的图象与y轴交于点B,若P是x轴上一点, 且满足△PAB的面积是4,
直接写出点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知A(3,0)、B(4,4)、原点O(0,0)在抛物线y=ax2+bx+c (a≠0)上.

(1)求抛物线的解析式.
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个交点D,求m的值及点D的坐标.
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P的坐标(点P、O、D分别与点N、O、B对应)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4.若用想x,y表示直角三角形的两直角边(x>y),则下列四个说法:①
 ,②x-y=2,③2xy+4=49,④x+y=9其中说法正确的是( )
,②x-y=2,③2xy+4=49,④x+y=9其中说法正确的是( )
A. ①②B. ①②③④C. ②④D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边分别为6和3,则此等腰三角形周长为____;已知等腰三角形的一个内角为50°,则它的顶角为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和40,则△EDF的面积为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.

(1)求直线AB的解析式;
(2)当点P运动到点(
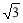 ,0)时,求此时DP的长及点D的坐标;
,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于
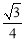 ?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
相关试题

