【题目】如图,在平面直角坐标系xoy中,函数![]() 的图象与一次函数y=kx-k的图象的交点为A(m,2).
的图象与一次函数y=kx-k的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)设一次函数y=kx-k的图象与y轴交于点B,若P是x轴上一点, 且满足△PAB的面积是4,
直接写出点P的坐标.

参考答案:
【答案】解:(1)将A(m,2)代入![]() 得,m=2,则A点坐标为A(2,2)。
得,m=2,则A点坐标为A(2,2)。
将A(2,2)代入y=kx-k得,2k-k=2,解得k=2。
∴一次函数解析式为y=2x-2。
(2)(3,0),(-1,0)。
【解析】反比例函数与一次函数的交点问题,曲线上点的坐标与方程的关系。
(1)将A点坐标代入![]() 求出m的值为2,再将(2,2)代入y=kx-k,求出k的值,即可得到一次函数的解析式。
求出m的值为2,再将(2,2)代入y=kx-k,求出k的值,即可得到一次函数的解析式。
(2)将三角形以x轴为分界线,分为两个三角形计算,再把它们相加:
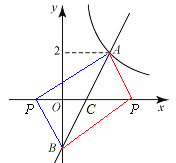
∵一次函数y=2x-2与x轴的交点为C(1,0),与y轴的交点为B(0,-2),
∴![]() ,解得CP=2。
,解得CP=2。
∴P点坐标为(3,0),(-1,0)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知: AB//CD, BP 和CP分别平分∠ABC和∠DCB,点E, F分别在AB和CD

(1)如图1, EF过点P,且与AB垂直,求证: PE=PF.
(2)如图2, EF过点P,求证: PE=PF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】台州某校七(1)班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据.
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少?
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时(结果保留一位小数)?





-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90° ,∠ACB=30° ,AD平分∠BAC, BD=
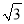 ,点P为线段AC上的一个动点
,点P为线段AC上的一个动点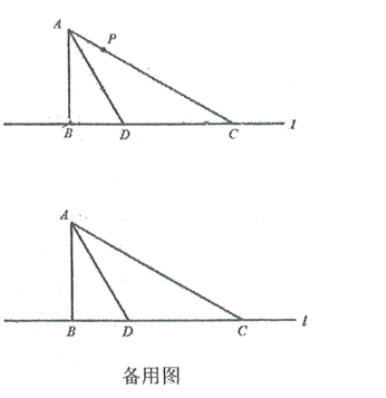
(1)求AC的长
(2)作△ABC中∠ACB的角平分线CH,求BH的长
(3)若点E在直线1上,且在C点的左侧,PE=PC, AP为多少时,△ACE为等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知A(3,0)、B(4,4)、原点O(0,0)在抛物线y=ax2+bx+c (a≠0)上.

(1)求抛物线的解析式.
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个交点D,求m的值及点D的坐标.
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P的坐标(点P、O、D分别与点N、O、B对应)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4.若用想x,y表示直角三角形的两直角边(x>y),则下列四个说法:①
 ,②x-y=2,③2xy+4=49,④x+y=9其中说法正确的是( )
,②x-y=2,③2xy+4=49,④x+y=9其中说法正确的是( )
A. ①②B. ①②③④C. ②④D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为5的正方形ABCD中,以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形的个数为( )

A.3B.4C.5D.6
相关试题

