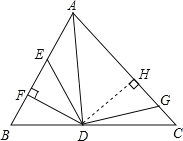
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和40,则△EDF的面积为______.

参考答案:
【答案】5.
【解析】
过点D作DH⊥AC于H,根据角平分线上的点到角的两边距离相等可得DF=DH,然后利用“HL”证明Rt△DEF和Rt△DGH全等,根据全等三角形的面积相等可得S△EDF=S△GDH,设△EDF的面积为S,然后根据S△ADF=S△ADH列出方程求解即可.
如图,过点D作DH⊥AC于H.
∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DH.
在Rt△DEF和Rt△DGH中,![]() ,
,
∴Rt△DEF≌Rt△DGH(HL),
∴S△EDF=S△GDH,
同理Rt△ADF≌Rt△ADH,
设△EDF的面积为S,
∴S△ADF=S△ADH,即40+S=50﹣S,
解得:S=5.
故答案为:5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小米利用暑期参加社会实践,在妈妈的帮助下,利用社区提供的免费摊点卖玩具,已知小米所有玩具的进价均2元
 个,在销售过程中发现:每天玩具销售量y件与销售价格x元
个,在销售过程中发现:每天玩具销售量y件与销售价格x元 件的关系如图所示,其中AB段为反比例函数图象的一部分,BC段为一次函数图象的一部分,设小米销售这种玩具的日利润为w元.
件的关系如图所示,其中AB段为反比例函数图象的一部分,BC段为一次函数图象的一部分,设小米销售这种玩具的日利润为w元. 根据图象,求出y与x之间的函数关系式;
根据图象,求出y与x之间的函数关系式; 求出每天销售这种玩具的利润
求出每天销售这种玩具的利润 元
元 与
与 元
元 件
件 之间的函数关系式,并求每天利润的最大值;
之间的函数关系式,并求每天利润的最大值; 若小米某天将价格定为超过4元
若小米某天将价格定为超过4元 ,那么要使得小米在该天的销售利润不低于54元,求该天玩具销售价格的取值范围.
,那么要使得小米在该天的销售利润不低于54元,求该天玩具销售价格的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有A、B、C三把锁,其中A锁配了一把钥匙a,B锁配了一把钥匙b,C锁配了一把钥匙c,对于每把锁,只有用所配的钥匙才能打开,请根据题意,解决下列问题.
 从三把钥匙中,随机选取一把,求所选钥匙恰好能打开C锁的概率.
从三把钥匙中,随机选取一把,求所选钥匙恰好能打开C锁的概率. 从三把锁和三把钥匙中,随机选取两边锁和两把钥匙,若用选取的钥匙开选取的锁,求只能打开一把锁的概率.
从三把锁和三把钥匙中,随机选取两边锁和两把钥匙,若用选取的钥匙开选取的锁,求只能打开一把锁的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】李明同学积极响应学校号召,利用假期参加了班级组织的“研学旅行”活动,在参观某红色景区时,李明站在台阶DF上发现了对面山坡BC上有一块竖立的标语牌AB,他在台阶顶端F处测得标语牌顶点A的仰角为
 ,标语牌底端B的仰角为
,标语牌底端B的仰角为 ,如图,已知台阶高EF为3米,山坡坡面BC的长为25米,山坡BC的坡度为1:
,如图,已知台阶高EF为3米,山坡坡面BC的长为25米,山坡BC的坡度为1: ,求标语牌AB的高度
,求标语牌AB的高度 结果精确到
结果精确到 米,参考数据
米,参考数据 ,
,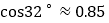 ,
,

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.正确的顺序是( )

①篮球运动员投篮时,投出去的篮球的高度与时间的关系
②去超市购买同一单价的水果,所付费用与水果数量的关系
③李老师使用的是一种含月租的手机计费方式,则他每月所付话费与通话时间的关系
④周末,小明从家到图书馆,看了一段时间书后,按原速度原路返回,小明离家的距离与时间的关系
A. ①②③④ B. ①③④② C. ①③②④ D. ①④②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=90°,已知△ABC中,AC=BC=13,AB=10,△ABC的顶点A、B分别在射线OM、ON上,当点B在ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:∠ACB是△ABC的一个内角.
求作:∠APB=∠ACB.
小明的做法如下:
如图
①作线段AB的垂直平分线m;
②作线段BC的垂直平分线n,与直线m交于点O;
③以点O为圆心,OA为半径作△ABC的外接圆;
④在弧ACB上取一点P,连结AP,BP.
所以∠APB=∠ACB.
老师说:“小明的作法正确.”
请回答:
(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是_____;
(2)∠APB=∠ACB的依据是_____.

相关试题

