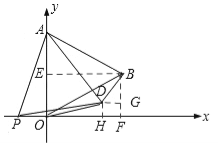
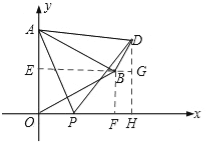
【题目】如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.

(1)求直线AB的解析式;
(2)当点P运动到点(![]() ,0)时,求此时DP的长及点D的坐标;
,0)时,求此时DP的长及点D的坐标;
(3)是否存在点P,使△OPD的面积等于![]() ?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】解:(1)如答图1,过点B作BE⊥y轴于点E,作BF⊥x轴于点F。
由已知得:BF=OE=2,∴![]() 。
。
∴点B的坐标是(![]() ,2)。
,2)。
设直线AB的解析式是y=kx+b(k≠0),则有
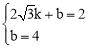 ,解得
,解得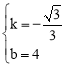 。
。
∴直线AB的解析式是![]() 。
。
(2)∵△ABD由△AOP旋转得到,
∴△ABD≌△AOP。∴AP=AD,∠DAB=∠PAO。
∴∠DAP=∠BAO=60°。∴△ADP是等边三角形。
∴![]() 。
。
如答图2,过点D作DH⊥x轴于点H,延长EB交DH于点G,则BG⊥DH。
在Rt△BDG中,∠BGD=90°,∠DBG=60°,
∴BG=BDcos60°=![]() .DG=BDsin60°=
.DG=BDsin60°=![]() 。
。
∴OH=EG=![]() ,DH=
,DH=![]() 。
。
∴点D的坐标为(![]() ,
,![]() )。
)。
(3)存在。
假设存在点P,在它的运动过程中,使△OPD的面积等于![]() 。
。
设点P为(t,0),下面分三种情况讨论:
①当t>0时,如答图2,BD=OP=t,DG=![]() t,∴DH=2+
t,∴DH=2+![]() t。
t。
∵△OPD的面积等于![]() ,∴
,∴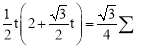 ,
,
解得![]() (舍去)。
(舍去)。
∴点P1的坐标为(![]() ,0)。
,0)。
②∵当D在x轴上时,如答图3,

根据锐角三角函数求出BD=OP=![]() ,
,
∴当![]() <t≤0时,如答图1,BD=OP=﹣t,DG=
<t≤0时,如答图1,BD=OP=﹣t,DG=![]() t,
t,
∴GH=BF=2﹣(![]() t)=2+
t)=2+![]() t。
t。
∵△OPD的面积等于![]() ,∴
,∴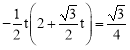 ,解得
,解得![]() 。
。
∴点P2的坐标为(![]() ,0),点P3的坐标为(
,0),点P3的坐标为(![]() ,0)。
,0)。
③当t≤![]() 时,如答图4,BD=OP=﹣t,DG=
时,如答图4,BD=OP=﹣t,DG=![]() t,
t,
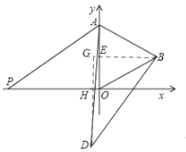
∴DH=![]() t﹣2。
t﹣2。
∵△OPD的面积等于![]() ,
,
∴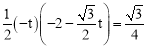 ,解得
,解得![]() (舍去)。
(舍去)。
∴点P4的坐标为(![]() ,0)。
,0)。
综上所述,点P的坐标分别为P1(![]() ,0)、P2(
,0)、P2(![]() ,0)、P3(
,0)、P3(![]() ,0)、
,0)、
P4(![]() ,0)。
,0)。
【解析】(1)过点B作BE⊥y轴于点E,作BF⊥x轴于点F.依题意得BF=OE=2,利用勾股定理求出OF,然后可得点B的坐标.设直线AB的解析式是y=kx+b,把已知坐标代入可求解。
(2)由△ABD由△AOP旋转得到,△ABD≌△AOP,AP=AD,∠DAB=∠PAO,∠DAP=∠BAO=60°,△ADP是等边三角形,利用勾股定理求出DP.在Rt△BDG中,∠BGD=90°,∠DBG=60°.利用三角函数求出BG=BDcos60°,DG=BDsin60°.然后求出OH,DH,然后求出点D的坐标。
(3)分三种情况进行讨论:
①当P在x轴正半轴上时,即t>0时;
②当P在x轴负半轴,但D在x轴上方时;即![]() <t≤0时
<t≤0时
③当P在x轴负半轴,D在x轴下方时,即t≤![]() 时。
时。
综合上面三种情况即可求出符合条件的t的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为5的正方形ABCD中,以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形的个数为( )

A.3B.4C.5D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边分别为6和3,则此等腰三角形周长为____;已知等腰三角形的一个内角为50°,则它的顶角为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和40,则△EDF的面积为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】给出一列数
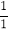 ,
, ,
,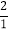 ,
, ,
, ,
,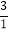 ,…,
,…, ,
,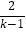 ,
,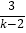 ,…,
,…,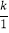 ,…,在这列数中,第50个值等于1的项的序号是( )
,…,在这列数中,第50个值等于1的项的序号是( )A. 4900 B. 4901 C. 5000 D. 5001
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数
 和一次函数y=k2x+b的图象交于点M(3,﹣
和一次函数y=k2x+b的图象交于点M(3,﹣ )和点N(﹣1,2),则k1=_____,k2=____,一次函数的图象交x轴于点_____.
)和点N(﹣1,2),则k1=_____,k2=____,一次函数的图象交x轴于点_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是 分米.

相关试题

