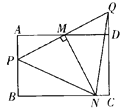
【题目】在矩形ABCD中,AB=8,AD=12,M是AD边的中点,P是AB边上的一个动点(不与A、B重合),PM的延长线交射线CD于Q点,MN⊥PQ交射线BC于N点。
(1)若点N在BC之间时,如图:
①求证:∠NPQ=∠PQN;
②请问![]() 是否为定值?若是定值,求出该定值;若不是,请举反例说明;
是否为定值?若是定值,求出该定值;若不是,请举反例说明;
(2)当△PBN与△NCQ的面积相等时,求AP的值.
参考答案:
【答案】(1)①证明见解析;②![]() 是定值,理由见解析;(2)AP=6
是定值,理由见解析;(2)AP=6
【解析】分析:(1)、①由矩形的性质证明△APM≌△QDM就可以得出PPM=QM,再由MN⊥PQ就可以得出结论;②作ME⊥BC于E,证明△AMP∽△EMN,由相似三角形的性质既可以求出PM与MN的关系,再由勾股定理表示出PN就可以求出结论;(2)、分两种情况,如图2,如图3,作BF⊥PN于F,CG⊥QN于G,作中线BS、CT,通过证明Rt△BFS≌Rt△CGT和△PBN≌△QCN,进一步由全等三角形的性质就可以得出结论.
详解:解(1)①证明:∵四边形ABCD是矩形,∴∠A=∠ADC=∠ADQ=90°,
AB//CD,∴∠APM=∠DQM, ∵M是AD边的中点,∴AM=DM,
在△APM和△DQM中,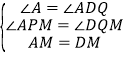 ,∴△APM≌△DQM(AAS),∴PM=QM,
,∴△APM≌△DQM(AAS),∴PM=QM,
∵MN⊥PQ,∴MN是线段PQ的垂直平分线,∴PN=QN,∴∠NPQ=∠PQN;
②解:![]() 是定值
是定值
理由:如图①,过点M作ME⊥BC于点E,∴∠MEN=∠MEB=∠AME=90°,
∴四边形ABEM是矩形,∠MEN=∠MAP,∴AB=EM,
∵MN⊥PQ,∴∠PMN=90°,∴∠PMN=∠AME,
∴∠PMN-∠PME=∠AME-∠PME,∴∠EMN=∠AMP, ∴△AMP∽△EMN,
∴![]() ,∴
,∴![]() ,∵AD=12,M是AD边的中点,∴AM=
,∵AD=12,M是AD边的中点,∴AM=![]() AD=6,
AD=6,
∵AB=8,∴![]() ;
;
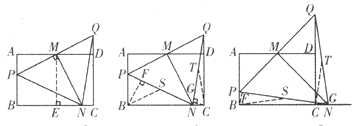
图① 图② 图③
(2)解:分点N在BC之间和点N在BC延长线上两种情况
(ⅰ)当点N在BC之间时,如图②,作BF⊥PN于点F,CG⊥QN于点G,再分别作Rt△PBN和Rt△NCQ的中线BS、CT, ∴∠BFS=∠CGT=90°,BS=![]() PN,CT=
PN,CT=![]() QN,
QN,
∵PN=QN,S△PBN=S△NCQ,∴BF=CG,BS=CT
在Rt△BFS和Rt△CGT中,![]() ,∴Rt△BFS≌Rt△CGT(HL),∴∠BSF=∠CTG,
,∴Rt△BFS≌Rt△CGT(HL),∴∠BSF=∠CTG,
∴∠BNP=![]() ∠BSF=
∠BSF=![]() ∠CTG=∠CQN,
∠CTG=∠CQN,
在△PBN和△NCQ中, ,∴△PBN≌△NCQ(AAS),∴BN=CQ,BP=CN,
,∴△PBN≌△NCQ(AAS),∴BN=CQ,BP=CN,
∵AP=AB-BP=8-CN,又∵CN=BC-BN=12-CQ,∴AP=CQ-4
又∵CQ=CD+DQ,DQ=AP,∴AP=4+AP(舍去),∴此种情况不成立;
(ⅱ)当点N在BC延长线上时,如图③,作BF⊥PN于点F,CG⊥QN于点G,再分别作Rt△PBN和Rt△NCQ的中线BS、CT, 同理可得,△PBN≌△NCQ,∴PB=NC,BN=CQ,
∵AP=DQ, ∵AP+8=DQ+CD=CQ=BC+CN=12+BP,
∴AP-BP=4 ①, ∵AP+BP=AB=8②, ①+②得:2AP=12,∴AP=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种空气净化器,每台净化器的成本价为200元.经过一段时间的销售发现,每月的销售量y(台)与销售单价x(元)的关系为y=﹣2x+800.
(1)该商店每月的利润为W元,写出利润W与销售单价x的函数关系式;
(2)若要使每月的利润为20000元,销售单价应定为多少元?
(3)商店要求销售单价不低于280元,也不高于350元,求该商店每月的最高利润和最低利润分别为多少?
-
科目: 来源: 题型:
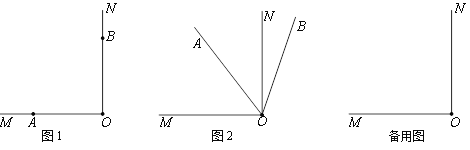
查看答案和解析>>【题目】如图1,∠MON=90°,点A,B分别在射线OM、ON上.将射线OA绕点O沿顺时针方向以每秒9°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒3°的速度旋转(如图2).设旋转时间为t(0≤t≤40,单位秒).
(1)当t=8时,∠AOB= °;
(2)在旋转过程中,当∠AOB=36°时,求t的值.
(3)在旋转过程中,当ON、OA、OB三条射线中的一条恰好平分另外两条射线组成的角(指大于0°而不超过180°的角)时,请求出t的值.
-
科目: 来源: 题型:
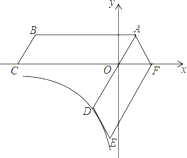
查看答案和解析>>【题目】如图,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,且AO:OD=1:2,点F恰好落在x轴的正半轴上,若点C(﹣6,0),点D在反比例函数y=
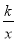 的图象上.
的图象上.(1)证明:△AOF是等边三角形,并求k的值;
(2)在x轴上有一点G,且△ACG是等腰三角形,求点G的坐标;
(3)求旋转过程中四边形ABCO扫过的面积;
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1,0),B(x2,0)(0<x1<x2)两点.
(1)若点A(0.5,0)和点B(1.5,0),求抛物线的表达式;
(2)三角形的内心是________的交点.在(1)的条件下,抛物线与y轴交于点C,点D在x轴上,且坐标为(-3,0),直线l经过点C、D.在抛物线上是否存在一点P,使△DCP的内心在y轴上,若存在,求出点P的坐标,若不存在,请说明理由;
(3)是否存在整数a,b,使得1<x1<2和1<x2<2同时成立?证明你的结论.
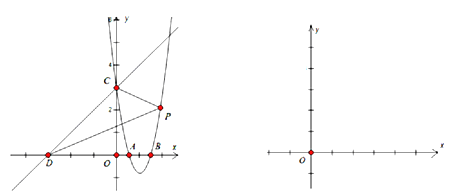
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“泰”、“兴”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“泰兴”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应集合的括号内.
+6.5,
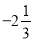 ,0.5,0,-3.2,13,-9,
,0.5,0,-3.2,13,-9,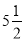 ,-1,-3.6
,-1,-3.6(1)正数集合:{ …};
(2)整数集合:{ …};
(3)非负数集合:{ …};
相关试题

