【题目】某商店经销一种空气净化器,每台净化器的成本价为200元.经过一段时间的销售发现,每月的销售量y(台)与销售单价x(元)的关系为y=﹣2x+800.
(1)该商店每月的利润为W元,写出利润W与销售单价x的函数关系式;
(2)若要使每月的利润为20000元,销售单价应定为多少元?
(3)商店要求销售单价不低于280元,也不高于350元,求该商店每月的最高利润和最低利润分别为多少?
参考答案:
【答案】(1)w=﹣2x2+1200x﹣160000;(2)要使每月的利润为20000元,销售单价应定为300;(3)最高利润为20000元,最低利润为15000元.
【解析】分析:(1)、根据销售利润=每天的销售量×(销售单价-成本价),即可列出函数关系式;(2)、令w=20000代入解析式,求出满足条件的x的值即可;(3)、根据(1)得到销售利润的关系式,利用配方法可求最大值.
详解:解:(1)由题意得:w=(x﹣200)y=(x﹣200)(﹣2x+800)=﹣2x2+1200x﹣160000;
(2)令w=﹣2x2+1200x﹣160000=﹣2(x﹣300)2+20000=20000, 解得:x=300,
故要使每月的利润为20000元,销售单价应定为300;
(3)∵y=﹣2x2+1200x﹣160000=﹣2(x﹣300)2+20000,又∵![]()
∴当x=300时,![]() =20000;当x=350时,
=20000;当x=350时,![]() =15000;
=15000;
故最高利润为20000元,最低利润为15000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个由正奇数排成的数阵.用如图所示的四边形框去框住四个数.

(1)若设框住四个数中左上角的数为n,则这四个数的和为 (用n的代数式表示);
(2)平行移动四边形框,若框住四个数的和为228,求出这4个数;
(3)平行移动四边形框,能否使框住四个数的和为508?若能,求出这4个数;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
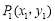 ,
,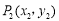 是平面直角坐标系中的任意两点,我们把
是平面直角坐标系中的任意两点,我们把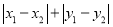 叫做
叫做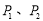 两点间的“直角距离”,记作
两点间的“直角距离”,记作 .
.(1)令
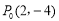 ,
,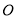 为坐标原点,则
为坐标原点,则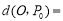 ________;
________; (2)已知
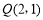 ,动点
,动点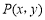 满足
满足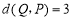 ,且
,且 均为整数:
均为整数:①满足条件的点
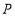 有多少个?
有多少个?②若点
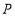 在直线
在直线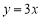 上,请写出符合条件的点
上,请写出符合条件的点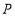 的坐标.
的坐标.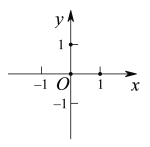
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三位数,百位数是
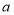 ,十位数是
,十位数是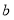 ,个位数是
,个位数是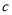 ,我们可以记作
,我们可以记作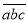 ,
, 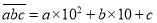 表示,例如
表示,例如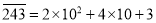 ,仿照上面的例子,
,仿照上面的例子,(1)
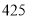 可以用 表示;
可以用 表示;(2)
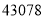 可以用 表示;
可以用 表示;(3)欧阳老师给4为同学玩一个数字游戏,先请A同学心里想一个三位数,并把这个三位数在纸上写两遍构成一个六位数交给B同学,如他心里想的是789,那么他在纸上写的就是789789,B把这个六位数除以7,得到的商写在另一张纸上并交给C同学,C同学把B同学给他的数字除以11,得到的商写在另一张纸上并交给D同学,D同学把C同学给他的数字除以13,得到的商写在另一张纸上,并交还给A同学,还给
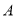 同学的数字和他刚开始想的数字有什么关系?并说明理由.
同学的数字和他刚开始想的数字有什么关系?并说明理由. -
科目: 来源: 题型:
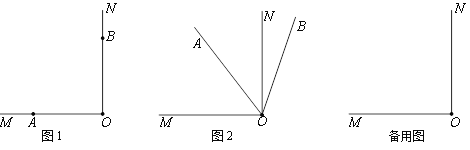
查看答案和解析>>【题目】如图1,∠MON=90°,点A,B分别在射线OM、ON上.将射线OA绕点O沿顺时针方向以每秒9°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒3°的速度旋转(如图2).设旋转时间为t(0≤t≤40,单位秒).
(1)当t=8时,∠AOB= °;
(2)在旋转过程中,当∠AOB=36°时,求t的值.
(3)在旋转过程中,当ON、OA、OB三条射线中的一条恰好平分另外两条射线组成的角(指大于0°而不超过180°的角)时,请求出t的值.
-
科目: 来源: 题型:
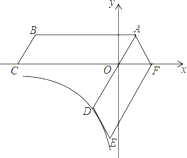
查看答案和解析>>【题目】如图,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,且AO:OD=1:2,点F恰好落在x轴的正半轴上,若点C(﹣6,0),点D在反比例函数y=
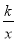 的图象上.
的图象上.(1)证明:△AOF是等边三角形,并求k的值;
(2)在x轴上有一点G,且△ACG是等腰三角形,求点G的坐标;
(3)求旋转过程中四边形ABCO扫过的面积;
-
科目: 来源: 题型:
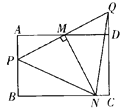
查看答案和解析>>【题目】在矩形ABCD中,AB=8,AD=12,M是AD边的中点,P是AB边上的一个动点(不与A、B重合),PM的延长线交射线CD于Q点,MN⊥PQ交射线BC于N点。
(1)若点N在BC之间时,如图:
①求证:∠NPQ=∠PQN;
②请问
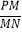 是否为定值?若是定值,求出该定值;若不是,请举反例说明;
是否为定值?若是定值,求出该定值;若不是,请举反例说明;(2)当△PBN与△NCQ的面积相等时,求AP的值.
相关试题

