【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“泰”、“兴”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“泰兴”的概率.
参考答案:
【答案】(1) ![]() ; (2)
; (2) ![]() .
.
【解析】试题分析:(1)由一个不透明的口袋里装有分别标有汉字“美”、“丽”、“泰”、“兴”的四个小球,除汉字不同之外,小球没有任何区别,直接利用概率公式求解即可求得答案;
(2)首先根据题意用表格列举出所有可能的结果与取出的两个球上的汉字恰能组成“美丽”或“泰兴”的情况,再利用概率公式即可求得答案.
试题解析:解:(1)∵有汉字“美”、“丽”、“泰”、“兴”的四个小球,任取一球,共有4种不同结果,∴球上汉字是“美”的概率为P=![]() ;
;
(2)列表如下:
美 | 丽 | 泰 | 兴 | |
美 | ---- | (丽,美) | (泰,美) | (兴,美) |
丽 | (美,丽) | ---- | (泰,丽) | (兴,丽) |
泰 | (美,泰) | (丽,泰) | ---- | (兴,泰) |
兴 | (美,兴) | (丽,兴) | (泰,兴) | ---- |
所有等可能的情况有12种,其中取出的个球上的汉字恰能组成“美丽”或“泰兴”的情况有4种,则P=![]() =
=![]() .
.
-
科目: 来源: 题型:
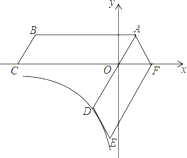
查看答案和解析>>【题目】如图,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,且AO:OD=1:2,点F恰好落在x轴的正半轴上,若点C(﹣6,0),点D在反比例函数y=
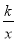 的图象上.
的图象上.(1)证明:△AOF是等边三角形,并求k的值;
(2)在x轴上有一点G,且△ACG是等腰三角形,求点G的坐标;
(3)求旋转过程中四边形ABCO扫过的面积;
-
科目: 来源: 题型:
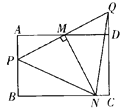
查看答案和解析>>【题目】在矩形ABCD中,AB=8,AD=12,M是AD边的中点,P是AB边上的一个动点(不与A、B重合),PM的延长线交射线CD于Q点,MN⊥PQ交射线BC于N点。
(1)若点N在BC之间时,如图:
①求证:∠NPQ=∠PQN;
②请问
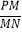 是否为定值?若是定值,求出该定值;若不是,请举反例说明;
是否为定值?若是定值,求出该定值;若不是,请举反例说明;(2)当△PBN与△NCQ的面积相等时,求AP的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1,0),B(x2,0)(0<x1<x2)两点.
(1)若点A(0.5,0)和点B(1.5,0),求抛物线的表达式;
(2)三角形的内心是________的交点.在(1)的条件下,抛物线与y轴交于点C,点D在x轴上,且坐标为(-3,0),直线l经过点C、D.在抛物线上是否存在一点P,使△DCP的内心在y轴上,若存在,求出点P的坐标,若不存在,请说明理由;
(3)是否存在整数a,b,使得1<x1<2和1<x2<2同时成立?证明你的结论.
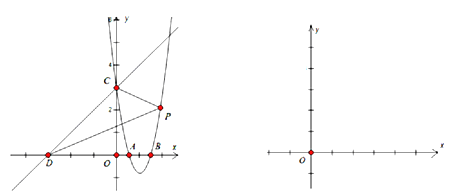
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应集合的括号内.
+6.5,
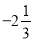 ,0.5,0,-3.2,13,-9,
,0.5,0,-3.2,13,-9,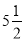 ,-1,-3.6
,-1,-3.6(1)正数集合:{ …};
(2)整数集合:{ …};
(3)非负数集合:{ …};
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(-2,2),B(8,12)在抛物线y=ax2+bx上.
(1)求抛物线的解析式;
(2)如图1,点F的坐标为(0,m)(m>4),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H,设抛物线与x轴的正半轴交于点E,连接FH、AE,求
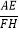 之值(用含m的代数式表示);
之值(用含m的代数式表示);(3)如图2,直线AB分别交x轴、y轴于C、D两点,点P从点C出发,沿射线CD方向匀速运动,速度为每秒
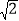 个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.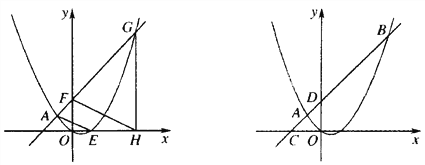
-
科目: 来源: 题型:
查看答案和解析>>【题目】某影院共有15排座位,第一排有12个座位数,从第2排开始,每一排都比前一排增加2个座位.
(1)请你在下表的空格里填写一个适当的式子.
第1排的座位数
第2排的座位数
第3排的座位数
…
第
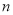 排的座位数
排的座位数12
14
16
…
(2)影院最后两排共有多少个座位?
相关试题

