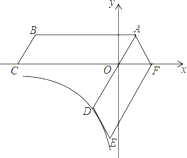
【题目】如图,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,且AO:OD=1:2,点F恰好落在x轴的正半轴上,若点C(﹣6,0),点D在反比例函数y=![]() 的图象上.
的图象上.
(1)证明:△AOF是等边三角形,并求k的值;
(2)在x轴上有一点G,且△ACG是等腰三角形,求点G的坐标;
(3)求旋转过程中四边形ABCO扫过的面积;
参考答案:
【答案】(1)证明见解析; k=![]() ; (2) ( 8, 0) ,(
; (2) ( 8, 0) ,(![]() ,0 ) (
,0 ) (![]() ),(
),(![]() ,0) ;(3) S=
,0) ;(3) S=![]() .
.
【解析】试题分析:(1)由旋转的性质可知AO=AF,且∠AOF=∠BAO=∠OAF,可证得△AOF为等边三角形,由题意可求得OA、OD的长,过D作DK⊥x轴于点K,则可求得OK和DK的长,可求得D点坐标,代入反比例函数解析式可求得k的值;
(2)设G(x,0),由A、C的坐标可分别表示出AG、CG和AC的长,分AG=CG、AG=AC和CG=AC三种情况分别得到关于x的方程,可求得x的值,则可求得G点坐标;
(3)过A作AH⊥x轴于H.可求得AH的长.由旋转角=∠CAE=∠OAF=60°,四边形ABCO扫过的面积=扇形CAE的面积+平行四边形ABCO的面积,即可得出结论.
试题解析:解:(1)过D作DK⊥x轴于K.由旋转的性质可得AO=AF=DE=BC,∠BAO=∠OAF.∵AB∥BC,∴∠BAO=∠AOF,∴∠AOF=∠OAF,∴AF=OF,∴AF=OF=OA,∴△AOF为等边三角形.设D(x,y).∵C(﹣6,0),∴OC=6,∴AD=CO=6.∵AO:OD=1:2,∴AO=2,OD=4.∵∠COD=∠AOF=60°,∴OK=![]() OD=2,DK=
OD=2,DK=![]() OK=
OK=![]() .∵x<0,y<0,∴x=-2,y=-
.∵x<0,y<0,∴x=-2,y=-![]() ,∴D(-2,-
,∴D(-2,- ![]() ),∴k=-2×(-
),∴k=-2×(-![]() )=
)=![]() .
.

(2)设G(x,0),且A(1, ![]() ),C(﹣6,0),∴AG=
),C(﹣6,0),∴AG=![]() =
=![]() ,CG=|x+6|,AC=
,CG=|x+6|,AC=![]() =
=![]() .∵△ACG是等腰三角形,∴有AG=CG、AG=AC和CG=AC三种情况:
.∵△ACG是等腰三角形,∴有AG=CG、AG=AC和CG=AC三种情况:
①当AG=CG时,则![]() =|x+6|,解得x=﹣
=|x+6|,解得x=﹣![]() ,此时G点坐标为(﹣
,此时G点坐标为(﹣![]() ,0);
,0);
②当AG=AC时,则![]() =
=![]() ,解得x=﹣6(与C点重合,舍去)或x=8,此时G点坐标为(8,0);
,解得x=﹣6(与C点重合,舍去)或x=8,此时G点坐标为(8,0);
③当CG=AC时,则|x+6|=![]() ,解得x=﹣6+
,解得x=﹣6+![]() 或x=﹣6﹣
或x=﹣6﹣![]() ,此时G点坐标为(﹣6+
,此时G点坐标为(﹣6+![]() ,0)或(﹣6﹣
,0)或(﹣6﹣![]() ,0);
,0);
综上可知G点坐标为(﹣![]() ,0)或(8,0)或(﹣6+
,0)或(8,0)或(﹣6+![]() ,0)或(﹣6﹣
,0)或(﹣6﹣![]() ,0);
,0);
(3)如图2,过A作AH⊥x轴于H.∵OA=2,∠AOH=60°,∴AH=AOsin60°=![]() =
=![]() .AC=
.AC=![]() ,旋转角=∠CAE=∠OAF=60°,四边形ABCO扫过的面积=扇形CAE的面积+平行四边形ABCO的面积=
,旋转角=∠CAE=∠OAF=60°,四边形ABCO扫过的面积=扇形CAE的面积+平行四边形ABCO的面积=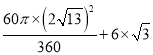 =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三位数,百位数是
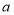 ,十位数是
,十位数是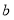 ,个位数是
,个位数是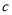 ,我们可以记作
,我们可以记作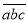 ,
, 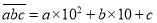 表示,例如
表示,例如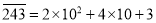 ,仿照上面的例子,
,仿照上面的例子,(1)
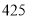 可以用 表示;
可以用 表示;(2)
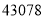 可以用 表示;
可以用 表示;(3)欧阳老师给4为同学玩一个数字游戏,先请A同学心里想一个三位数,并把这个三位数在纸上写两遍构成一个六位数交给B同学,如他心里想的是789,那么他在纸上写的就是789789,B把这个六位数除以7,得到的商写在另一张纸上并交给C同学,C同学把B同学给他的数字除以11,得到的商写在另一张纸上并交给D同学,D同学把C同学给他的数字除以13,得到的商写在另一张纸上,并交还给A同学,还给
 同学的数字和他刚开始想的数字有什么关系?并说明理由.
同学的数字和他刚开始想的数字有什么关系?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种空气净化器,每台净化器的成本价为200元.经过一段时间的销售发现,每月的销售量y(台)与销售单价x(元)的关系为y=﹣2x+800.
(1)该商店每月的利润为W元,写出利润W与销售单价x的函数关系式;
(2)若要使每月的利润为20000元,销售单价应定为多少元?
(3)商店要求销售单价不低于280元,也不高于350元,求该商店每月的最高利润和最低利润分别为多少?
-
科目: 来源: 题型:
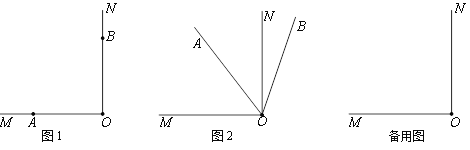
查看答案和解析>>【题目】如图1,∠MON=90°,点A,B分别在射线OM、ON上.将射线OA绕点O沿顺时针方向以每秒9°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒3°的速度旋转(如图2).设旋转时间为t(0≤t≤40,单位秒).
(1)当t=8时,∠AOB= °;
(2)在旋转过程中,当∠AOB=36°时,求t的值.
(3)在旋转过程中,当ON、OA、OB三条射线中的一条恰好平分另外两条射线组成的角(指大于0°而不超过180°的角)时,请求出t的值.
-
科目: 来源: 题型:
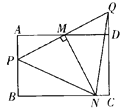
查看答案和解析>>【题目】在矩形ABCD中,AB=8,AD=12,M是AD边的中点,P是AB边上的一个动点(不与A、B重合),PM的延长线交射线CD于Q点,MN⊥PQ交射线BC于N点。
(1)若点N在BC之间时,如图:
①求证:∠NPQ=∠PQN;
②请问
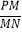 是否为定值?若是定值,求出该定值;若不是,请举反例说明;
是否为定值?若是定值,求出该定值;若不是,请举反例说明;(2)当△PBN与△NCQ的面积相等时,求AP的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1,0),B(x2,0)(0<x1<x2)两点.
(1)若点A(0.5,0)和点B(1.5,0),求抛物线的表达式;
(2)三角形的内心是________的交点.在(1)的条件下,抛物线与y轴交于点C,点D在x轴上,且坐标为(-3,0),直线l经过点C、D.在抛物线上是否存在一点P,使△DCP的内心在y轴上,若存在,求出点P的坐标,若不存在,请说明理由;
(3)是否存在整数a,b,使得1<x1<2和1<x2<2同时成立?证明你的结论.
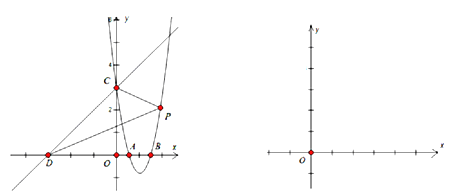
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“泰”、“兴”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“泰兴”的概率.
相关试题

