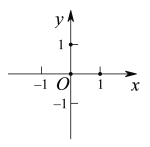
【题目】![]() ,
,![]() 是平面直角坐标系中的任意两点,我们把
是平面直角坐标系中的任意两点,我们把![]() 叫做
叫做![]() 两点间的“直角距离”,记作
两点间的“直角距离”,记作![]() .
.
(1)令![]() ,
,![]() 为坐标原点,则
为坐标原点,则![]() ________;
________;
(2)已知![]() ,动点
,动点![]() 满足
满足![]() ,且
,且![]() 均为整数:
均为整数:
①满足条件的点![]() 有多少个?
有多少个?
②若点![]() 在直线
在直线![]() 上,请写出符合条件的点
上,请写出符合条件的点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)6;(2)①12个;②![]()
【解析】
(1)根据“直角距离”的定义,将P0(2,-4),O(0,0)点的坐标代入即可求得结果;
(2)根据“直角距离”的定义,将Q(2,1),动点P(x,y)的坐标代入可得知|2-x|+|1-y|=3,因为x、y均为正数,所以坐标不多,可一一分析列举出来,即可解决问题.
解:(1)d(O,P0)=|0-2|+|0-(-4)|=2+4=6.
故答案为:6.
(2)①∵d(Q,P)=|2-x|+|1-y|=3,且x、y均为整数,
∴当|1-y|=0时,|2-x|=3,解得P点坐标为(-1,1)、(5,1);
当|1-y|=1时,|2-x|=2,解得P点坐标为(0,0)、(4,0)、(0,2)、(4,2);
当|1-y|=2时,|2-x|=1,解得P点坐标为(1,-1)、(3,-1)、(1,3)、(3,3);
当|1-y|=3时,|2-x|=0,解得P点坐标为(2,-2)、(2,4).
综上,得知满足条件的点P的坐标有12个.
②直线y=3x上的点有纵坐标是横坐标3倍的特点,
∴符合条件的点P的坐标为(0,0)和(1,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,﹣1),交双曲线y=
 于点C、D.
于点C、D.(1)求k、b的值;
(2)写出不等式kx+b>
 的解集.
的解集.
-
科目: 来源: 题型:
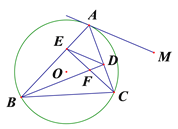
查看答案和解析>>【题目】如图,△ABC是⊙O的内接三角形,CE⊥AB于点E,BD⊥AC于点D,BD、CE相交于点F,连结ED.
(1)若∠ABC=45°,证明AE=EF;
(2)求证:△AED∽△ACB;
(3)过点A的直线AM∥ED, AM是⊙O的切线吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个由正奇数排成的数阵.用如图所示的四边形框去框住四个数.

(1)若设框住四个数中左上角的数为n,则这四个数的和为 (用n的代数式表示);
(2)平行移动四边形框,若框住四个数的和为228,求出这4个数;
(3)平行移动四边形框,能否使框住四个数的和为508?若能,求出这4个数;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三位数,百位数是
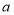 ,十位数是
,十位数是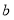 ,个位数是
,个位数是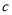 ,我们可以记作
,我们可以记作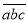 ,
, 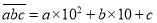 表示,例如
表示,例如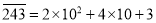 ,仿照上面的例子,
,仿照上面的例子,(1)
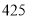 可以用 表示;
可以用 表示;(2)
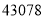 可以用 表示;
可以用 表示;(3)欧阳老师给4为同学玩一个数字游戏,先请A同学心里想一个三位数,并把这个三位数在纸上写两遍构成一个六位数交给B同学,如他心里想的是789,那么他在纸上写的就是789789,B把这个六位数除以7,得到的商写在另一张纸上并交给C同学,C同学把B同学给他的数字除以11,得到的商写在另一张纸上并交给D同学,D同学把C同学给他的数字除以13,得到的商写在另一张纸上,并交还给A同学,还给
 同学的数字和他刚开始想的数字有什么关系?并说明理由.
同学的数字和他刚开始想的数字有什么关系?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种空气净化器,每台净化器的成本价为200元.经过一段时间的销售发现,每月的销售量y(台)与销售单价x(元)的关系为y=﹣2x+800.
(1)该商店每月的利润为W元,写出利润W与销售单价x的函数关系式;
(2)若要使每月的利润为20000元,销售单价应定为多少元?
(3)商店要求销售单价不低于280元,也不高于350元,求该商店每月的最高利润和最低利润分别为多少?
-
科目: 来源: 题型:
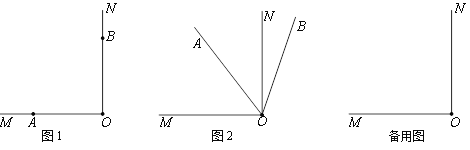
查看答案和解析>>【题目】如图1,∠MON=90°,点A,B分别在射线OM、ON上.将射线OA绕点O沿顺时针方向以每秒9°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒3°的速度旋转(如图2).设旋转时间为t(0≤t≤40,单位秒).
(1)当t=8时,∠AOB= °;
(2)在旋转过程中,当∠AOB=36°时,求t的值.
(3)在旋转过程中,当ON、OA、OB三条射线中的一条恰好平分另外两条射线组成的角(指大于0°而不超过180°的角)时,请求出t的值.
相关试题

