【题目】如图,点A的坐标是(﹣2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.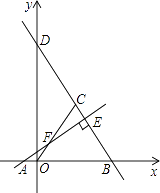
(1)求直线BD的函数表达式;
(2)求线段OF的长;
(3)连接BF,OE,试判断线段BF和OE的数量关系,并说明理由.
参考答案:
【答案】
(1)
解:∵△OBC是等边三角形,
∴∠OBC=60°,OC=BC=OB,
∵点B的坐标为(6,0),
∴OB=6,
在Rt△OBD中,∠OBC=60°,OB=6,
∴∠ODB=30°,
∴BD=12,
∴OD= ![]() =6
=6 ![]() ,
,
∴点D的坐标为(0,6 ![]() ),
),
设直线BD的解析式为y=kx+b,则可得 ![]() ,
,
解得: ![]() ,
,
∴直线BD的函数解析式为y=﹣ ![]() x+6
x+6 ![]()
(2)
解:∵∠OCB=60°,∠CEF=90°,
∴∠CFE=30°,
∴∠AFO=30°(对顶角相等),
又∵∠OBC=60°,∠AEB=90°,
∴∠BAE=30°,
∴∠BAE=∠AFO,
∴OF=OA=2
(3)
解:连接BF,OE,如图所示:
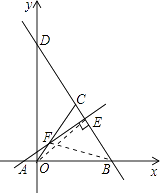
∵A(﹣2,0),B(6,0),
∴AB=8,
在Rt△ABE中,∠ABE=60°,AB=8,
∴BE= ![]() AB=4,
AB=4,
∴CE=BC﹣BE=2,
∴OF=CE=2,
在△COE和△OBF中, 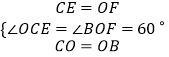 ,
,
∴△COE≌△OBF(SAS),
∴OE=BF.
【解析】(1)根据△OBC是等边三角形,可得∠OBC=60°,在Rt△PBD中,解得OD的长度,得出点D的坐标,利用待定系数法求出直线BD的解析式即可;(2)分别求出∠BAE和∠AFO的度数,即可得出OF=OA=2.(3)在Rt△ABE中,先求出BE,继而得出CE=OF,证明△COE≌△OBF,可得BF和OE的数量关系.
【考点精析】利用一次函数的图象和性质对题目进行判断即可得到答案,需要熟知一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.
-
科目: 来源: 题型:
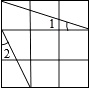
查看答案和解析>>【题目】如图,在3×3的正方形网格中标出了∠1和∠2。则∠1+∠2=。
-
科目: 来源: 题型:
查看答案和解析>>【题目】求x的值:(2x-3)2=36.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式2ax4+5ax3-13x2-x4+2021+2x+bx3-bx4-13x3是二次多项式,则a2+b2=。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】设x1 , x2 , x3 , x4 , x5 , x6 , x7是自然数,且x1<x2<x3<x4<x5<x6<x7 , x1+x2=x3 , x2+x3=x4 , x3+x4=x5 , x4+x5=x6 , x5+x6=x7 , 又x1+x2+x3+x4+x5+x6+x7=2010,那么x1+x2+x3的值最大是。
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式与不等式组
(1)求不等式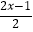 ﹣
﹣ 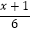 ≤1的解集.
≤1的解集.
(2)解不等式组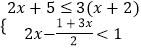 ,把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.
,把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.
相关试题

