【题目】已知多项式2ax4+5ax3-13x2-x4+2021+2x+bx3-bx4-13x3是二次多项式,则a2+b2=。
参考答案:
【答案】13
【解析】解:∵2ax4+5ax3-13x2-x4+2021+2x+bx3-bx4-13x3=(2a-b-1)x ![]() +(5a-13+b)x
+(5a-13+b)x ![]() -13x
-13x ![]() +2x+2021,
+2x+2021,
又∵此多项式为二次多项式,
∴ ![]() ,
,
解得 ![]() .
.
所以a ![]() +b
+b ![]() =2
=2 ![]() +3
+3 ![]() =13.
=13.
故答案为13.
将多项式2ax4+5ax3-13x2-x4+2021+2x+bx3-bx4-13x3进行合并得出(2a-b-1)x 4 +(5a-13+b)x 3 -13x 2 +2x+2021,又根据此多项式是二次多项式,从而得出关于a,b的方程,2a-b-1=0,5a-13+b=0;解它们组成的方程组,即可得出a,b的值,再代入代数式计算出结果即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在等边△ABC中,点D是BC边的中点,点P为AB 边上的一个动点,设AP=
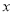 ,PD=
,PD= 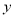 ,若
,若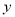 与
与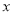 之间的函数关系的图象如图2所示,则等边△ABC的面积为( )
之间的函数关系的图象如图2所示,则等边△ABC的面积为( )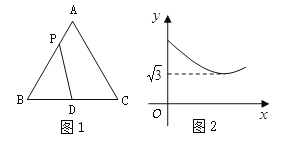
A. 4 B.
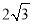 C. 12 D.
C. 12 D. 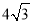
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在3×3的正方形网格中标出了∠1和∠2。则∠1+∠2=。
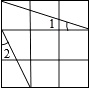
-
科目: 来源: 题型:
查看答案和解析>>【题目】求x的值:(2x-3)2=36.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标是(﹣2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.
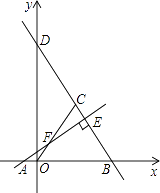
(1)求直线BD的函数表达式;
(2)求线段OF的长;
(3)连接BF,OE,试判断线段BF和OE的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】设x1 , x2 , x3 , x4 , x5 , x6 , x7是自然数,且x1<x2<x3<x4<x5<x6<x7 , x1+x2=x3 , x2+x3=x4 , x3+x4=x5 , x4+x5=x6 , x5+x6=x7 , 又x1+x2+x3+x4+x5+x6+x7=2010,那么x1+x2+x3的值最大是。
相关试题

