【题目】设x1 , x2 , x3 , x4 , x5 , x6 , x7是自然数,且x1<x2<x3<x4<x5<x6<x7 , x1+x2=x3 , x2+x3=x4 , x3+x4=x5 , x4+x5=x6 , x5+x6=x7 , 又x1+x2+x3+x4+x5+x6+x7=2010,那么x1+x2+x3的值最大是。
参考答案:
【答案】236
【解析】解:∵x1+x2=x3 , x2+x3=x4 , x3+x4=x5 , x4+x5=x6 , x5+x6=x7;x1+x2+x3+x4+x5+x6+x7=2010;
∴x1+x2+x3+x4+x5+x6+x7=13x1+20x2=2010,
∵x1x2是自然数,2010-13x1要能被20整除,且x1<x2
可得![]() ,
,![]() ,
,![]() ,
,
(x1+x2+x3)max=2(x1+x2)max=2(50+68)=236.
故答案为:236
根据x1+x2=x3 , x2+x3=x4 , x3+x4=x5 , x4+x5=x6 , x5+x6=x7;x1+x2+x3+x4+x5+x6+x7=2010;从而得出方程x1+x2+x3+x4+x5+x6+x7=13x1+20x2=2010,又根据x1x2是自然数,2010-13x1要能被20整除,且x1<x2,从而得出满足条件的所有值,再根据x1+x2+x3=2(x1+x2)算出答案,比较得出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式2ax4+5ax3-13x2-x4+2021+2x+bx3-bx4-13x3是二次多项式,则a2+b2=。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标是(﹣2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.
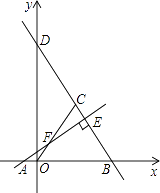
(1)求直线BD的函数表达式;
(2)求线段OF的长;
(3)连接BF,OE,试判断线段BF和OE的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式与不等式组
(1)求不等式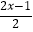 ﹣
﹣ 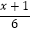 ≤1的解集.
≤1的解集.
(2)解不等式组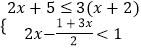 ,把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.
,把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).

①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②请画出△ABC关于原点对称的△A2B2C2 , 并写出点A2、B2、C2坐标;
③请画出△ABC绕原点O逆时针旋转90°后△A3B3C3 , 并写出点A3、B3、C3坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个角补角比它的余角的2倍多30°,这个角的度数为_____.
相关试题

