【题目】解不等式与不等式组
(1)求不等式 ![]() ﹣
﹣ ![]() ≤1的解集.
≤1的解集.
(2)解不等式组 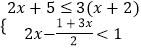 ,把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.
,把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.
参考答案:
【答案】
(1)解:3(2x﹣1)﹣(x+1)≤6,
6x﹣3﹣x﹣1≤6,
5x≤10,
x≤2
(2)解:解不等式①得:x≥﹣1,
解不等式②得:x<3,
所以不等式组的解集为:﹣1≤x<3,
所以非负整数解为:0,1,2.
在数轴上表示为: ![]()
【解析】(1)根据不等式的解法计算即可;(2)分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集即可,再找出解集范围内的非负整数即可.
【考点精析】通过灵活运用不等式的解集在数轴上的表示和一元一次不等式的解法,掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标是(﹣2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.
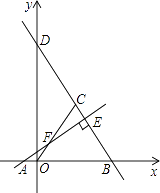
(1)求直线BD的函数表达式;
(2)求线段OF的长;
(3)连接BF,OE,试判断线段BF和OE的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】设x1 , x2 , x3 , x4 , x5 , x6 , x7是自然数,且x1<x2<x3<x4<x5<x6<x7 , x1+x2=x3 , x2+x3=x4 , x3+x4=x5 , x4+x5=x6 , x5+x6=x7 , 又x1+x2+x3+x4+x5+x6+x7=2010,那么x1+x2+x3的值最大是。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).

①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②请画出△ABC关于原点对称的△A2B2C2 , 并写出点A2、B2、C2坐标;
③请画出△ABC绕原点O逆时针旋转90°后△A3B3C3 , 并写出点A3、B3、C3坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个角补角比它的余角的2倍多30°,这个角的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC,∠BAC的平分线AE交BC于点D,且AE⊥BE.
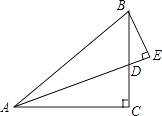
(1)求∠DBE的大小;
(2)求证:AD=2BE.
相关试题

