【题目】如图,在3×3的正方形网格中标出了∠1和∠2。则∠1+∠2=。 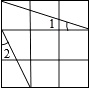
参考答案:
【答案】45°
【解析】解 :连接AC,BC .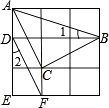
根据勾股定理,AC=BC=![]() ;AB=
;AB=![]()
∵(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2 ,
)2 ,
∴△ABC是等腰直角三角形,
∴∠ACB=90,∠CAB=45.
∵AD∥CF,AD=CF,
∴四边形ADFC是平行四边形,
∴AC∥DF,
∴∠2=∠DAC;
在Rt△ABD中,
∠1+∠DAB=90;
又∵∠DAB=∠DAC+∠CAB,
∴∠1+∠CAB+∠DAC=90 ,
∴∠1+∠DAC=45 ,
∴∠1+∠2=∠1+∠DAC=45.
故答案为:45.
连接AC,BC ;利用方格纸的特点,根据勾股定理得出AC,BC,AB的长, 然后根据勾股定理的逆定理判断出 △ABC是等腰直角三角形,从而得出 ∠ACB=90,∠CAB=45.根据一组对边平行且相等的四边形是平行四边形得出 四边形ADFC是平行四边形,根据平行四边形的对边平行得出AC∥DF,根据二直线平行同位角相等得出∠2=∠DAC;根据直角三角形两锐角互余得出∠1+∠DAB=90;,根据角的和差及等量代换得出∠1+∠2=∠1+∠DAC=45.
-
科目: 来源: 题型:
查看答案和解析>>【题目】In right Fig.,if the length of the segment AB is 1,M is the midpoint of the segment AB,and point C divides the segment MB into two parts such that MC:CB=1:2,then the length of AC is 。
(英汉词典:length 长度;segment 线段;midpoint 中点;divides…into 分为,分成)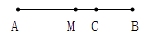
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有甲种原料360kg,乙种原料290kg,计划用这两种原料生产A、B两种产品共50件,已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg,可获利润700元;生产一件B种产品,需用甲种原料4kg,乙种原料10kg,可获利润1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润是W(元),采用哪种生产方案获总利润最大?最大利润为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在等边△ABC中,点D是BC边的中点,点P为AB 边上的一个动点,设AP=
 ,PD=
,PD= 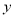 ,若
,若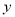 与
与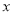 之间的函数关系的图象如图2所示,则等边△ABC的面积为( )
之间的函数关系的图象如图2所示,则等边△ABC的面积为( )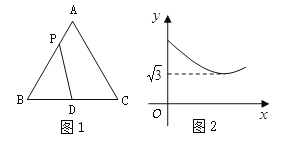
A. 4 B.
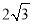 C. 12 D.
C. 12 D. 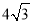
-
科目: 来源: 题型:
查看答案和解析>>【题目】求x的值:(2x-3)2=36.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式2ax4+5ax3-13x2-x4+2021+2x+bx3-bx4-13x3是二次多项式,则a2+b2=。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标是(﹣2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.
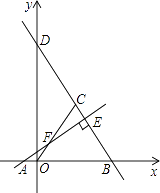
(1)求直线BD的函数表达式;
(2)求线段OF的长;
(3)连接BF,OE,试判断线段BF和OE的数量关系,并说明理由.
相关试题

