【题目】如图,平行四边形ABCD的面积是16,对角线AC、BD相交于点O,点M1、N1、P1分别为线段OD、DC、CO的中点,顺次连接M1N1、N1 P1、P1M1得到第一个△P1M1N1 , 面积为S1 , 分别取M1N1、N1P1、P1M1三边的中点P2、M2、N2 , 得到第二个△P2M2N2 , 面积记为S2 , 如此继续下去得到第n个△PnMnNn , 面积记为Sn , 则Sn﹣Sn﹣1= . (用含n的代数式表示,n≥2,n为整数)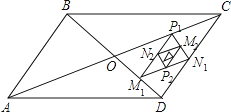
参考答案:
【答案】![]()
【解析】解:∵平行四边形ABCD被对角线所分的四个小三角形面积相等,∴S△OCD=16× ![]() =4,
=4,
∵M1、N1、P1分别为各边中点,故将△OCD分为四个面积相等的三角形,
∴S△M1N1P1=4× ![]() =1,依次往下,M2、N2、P2又将△M1N1P1的面积分为相等四分,故S2=S△M2N2P2=
=1,依次往下,M2、N2、P2又将△M1N1P1的面积分为相等四分,故S2=S△M2N2P2= ![]() S△M1N1P1=4×
S△M1N1P1=4× ![]() ×
× ![]() =4×
=4× ![]() ,
,
依此类推…
∴Sn=4× ![]() ,∴Sn﹣1=4×
,∴Sn﹣1=4× ![]() ,∴Sn﹣Sn﹣1=4×
,∴Sn﹣Sn﹣1=4× ![]() ﹣4×
﹣4× ![]() =﹣
=﹣ ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,结果正确的是( )
A.(﹣2y)3=﹣6y3
B.(﹣ab2)3=﹣ab6
C.(﹣a)3÷(﹣a2)=a
D.( )﹣1﹣22=2
)﹣1﹣22=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小浩从二次函数y=ax2+bx+c(a≠0)的图象中得到如下信息:
①ab<0
②4a+b=0
③当y=5时只能得x=0
④关于x的一元二次方程ax2+bx+c=10有两个不相等的实数根,
你认为其中正确的有( )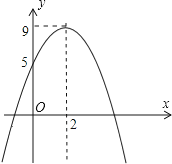
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】有若干个数,第一个数记为a1,第二个数记为a2,第三个数记为a3,…,第n个数记为an,若a1=
 ,从第二个数起,每个数都等于“1与它前面那个数差的倒数”.
,从第二个数起,每个数都等于“1与它前面那个数差的倒数”.(1)计算:a2 ,a3 ,a4 ,a5的值;
(2)这排数有什么规律?由你发现的规律,计算a2014的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l∥AB,l与AB之间的距离为2.C、D是直线l上两个动点(点C在D点的左侧),且AB=CD=5.连接AC、BC、BD,将△ABC沿BC折叠得到△A′BC.下列说法:①四边形ABCD的面积始终为10;②当A′与D重合时,四边形ABDC是菱形;③当A′与D不重合时,连接A′、D,则∠CA′D+∠BCA′=180°;④若以A′、C、B、D为顶点的四边形为矩形,则此矩形相邻两边之和为3
 或7.其中正确的是( )
或7.其中正确的是( )
A. ①②④ B. ①③④ C. ①②③ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了贯彻教育部关于中小学生“每天锻炼一小时”的要求,某市教育局做了一次随机抽样调查,其内容是:(1)学生每天锻炼时间是否达到1小时;(2)学生每天锻炼时间未达到1小时的原因.随机调查了600名学生,把所得的数据制成了如下的扇形统计图和条形统计图(不完整)
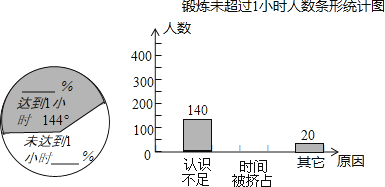
根据图示,回答以下问题:
(1)每天锻炼时间达到1小时的人数占被调查总人数的百分比是;
每天锻炼时间未达到1小时的人数占被调查总人数的百分比是;
每天锻炼时间未达到1小时的人数为人,其中原因是“时间被挤占”的人数是人;
(2)补全扇形统计图和条形统计图;
(3)若该市现有中小学生约27万人,据此调查,可估计今年该市中小学生每天锻炼未达到1小时的学生约有多少万人?
(4)从这次接受调查的学生中,随机抽取一名学生的“每天锻炼一小时”的情况,回答内容为“时间被挤占”的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】我市大力发展绿色交通,构建公共绿色交通体系,“共享单车”的投入使用给人们的出行带来便利.小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图统计图,请根据图中信息,解答下列问题:


(1)这次被调查的总人数是______;
(2)补全条形统计图;
(3)在扇形统计图中,求表示A组(t≤10分)的扇形圆心角的度数;
(4)如果骑共享单车的平均速度为12km/h,请估算,在租用共享单车的市民中,骑车路程不超过6km的人数所占的百分比.
相关试题

