搜索
【题目】如图，小浩从二次函数y=ax2+bx+c（a≠0）的图象中得到如下信息：
①ab＜0
②4a+b=0
③当y=5时只能得x=0
④关于x的一元二次方程ax2+bx+c=10有两个不相等的实数根，
你认为其中正确的有（ ）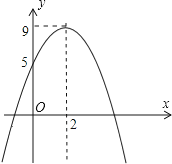
A.1个
B.2个
C.3个
D.4个
参考答案：
【答案】B
【解析】解：∵抛物线开口向下，
∴a＜0，
∵抛物线的对称轴为直线x=﹣ 
=2，
∴b=﹣4a，
∴b＞0，b+4a=0，所以①②正确；
∵抛物线的对称轴为直线x=2，
∴（0，5）和（4，5）是抛物线上两对称点，
∴x=0或4时，y=5，所以③错误；
∵抛物线的顶点坐标为（2，9），
∴y的最大值为9，
∴ax2+bx+c≤9，
∴一元二次方程ax2+bx+c=10无实数解，所以④错误．
故选B．
【考点精析】通过灵活运用二次函数图象以及系数a、b、c的关系，掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知四边形ABCD为正方形，AB=
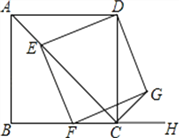
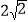，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE．交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．①求证：矩形DEFG是正方形；
②探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：
把两个相同的数连接在一起就得到一个新数，我们把它称为“连接数”，例如：234234，3939…等，都是连接数，其中，234234称为六位连接数，3939称为四位连接数．
（1）请写出一个六位连接数 ，它 （填“能”或“不能”）被13整除．
（2）是否任意六位连接数，都能被13整除，请说明理由．
（3）若一个四位连接数记为M，它的各位数字之和的3倍记为N，M﹣N的结果能被13整除，这样的四位连接数有几个？
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列运算中，结果正确的是（ ）
A.（﹣2y）3=﹣6y3
B.（﹣ab2）3=﹣ab6
C.（﹣a）3÷（﹣a2）=a
D.（
）﹣1﹣22=2 -
科目： 来源： 题型：
查看答案和解析>>【题目】有若干个数，第一个数记为a1，第二个数记为a2，第三个数记为a3，…，第n个数记为an，若a1=
，从第二个数起，每个数都等于“1与它前面那个数差的倒数”.(1)计算：a2 ，a3 ，a4 ，a5的值；
(2)这排数有什么规律？由你发现的规律，计算a2014的值.
-
科目： 来源： 题型：
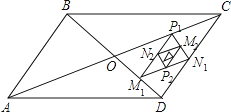
查看答案和解析>>【题目】如图，平行四边形ABCD的面积是16，对角线AC、BD相交于点O，点M1、N1、P1分别为线段OD、DC、CO的中点，顺次连接M1N1、N1 P1、P1M1得到第一个△P1M1N1 ， 面积为S1 ， 分别取M1N1、N1P1、P1M1三边的中点P2、M2、N2 ， 得到第二个△P2M2N2 ， 面积记为S2 ， 如此继续下去得到第n个△PnMnNn ， 面积记为Sn ， 则Sn﹣Sn﹣1= ． （用含n的代数式表示，n≥2，n为整数）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线l∥AB，l与AB之间的距离为2．C、D是直线l上两个动点（点C在D点的左侧），且AB=CD=5．连接AC、BC、BD，将△ABC沿BC折叠得到△A′BC．下列说法：①四边形ABCD的面积始终为10；②当A′与D重合时，四边形ABDC是菱形；③当A′与D不重合时，连接A′、D，则∠CA′D+∠BCA′=180°；④若以A′、C、B、D为顶点的四边形为矩形，则此矩形相邻两边之和为3
或7．其中正确的是（ ）
A. ①②④ B. ①③④ C. ①②③ D. ①②③④
相关试题
