【题目】如图,在△ABC 中,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)若∠1=∠2,试说明DG∥BC.
(2)若CD 平分∠ACB,∠A=60°,求∠B的度数.

参考答案:
【答案】(1)证明见解析;(2)∠B=60°.
【解析】
(1)根据垂直于同一条直线的两直线平行,先判定EF∥CD,根据两直线平行同位角相等,得∠1=∠BCD;根据等量代换可得∠DCB=∠2,从而根据内错角相等,两直线平行得证;
(2)根据CD⊥AB得出∠ADC的度数,从而求出∠ACD的度数,再根据CD平分∠ACB,进而求出∠ACB的度数,再根据三角形内角和定理,可得∠B的度数,.
(1)∵CD⊥AB,EF⊥AB
∴∠EFB=90°,∠CDB=90°
∴∠EFB=∠CDB
∴EF∥CD
∴∠1=∠BCD
∵∠1=∠2
∴∠2=∠BCD
∴DG∥BC
(2)∵CD⊥AB,
∴∠CDA=90°,
∵∠A=60°,
∴∠ACD=30°,
∵CD平分∠ACB,
∴∠ACD=![]() ∠ACB,
∠ACB,
∴∠ACB=60°,
∵∠A=60°,
∴∠B=180°-∠ACB-∠A=60°.
-
科目: 来源: 题型:
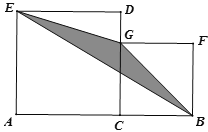
查看答案和解析>>【题目】如图,点C是线段AB上的一点,分别以AC.BC为边在AB的同侧作正方形ACDE和正方形CBFG,连接EG.BG.BE,当BC=1时,△BEG的面积记为S1,当BC=2时,△BEG的面积记为S2,……,以此类推,当BC=n时,△BEG的面积记为Sn,则S2020-S2019的值为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△A′B′C′,
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC在整个平移过程中线段AC扫过的面积为________.
(3)能使S△MBC=S△ABC的格点M共有_______个(点M异于点A)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
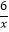 (x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣
(x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣ 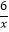 <0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )
<0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )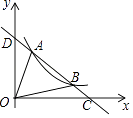
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④
 与EF相切;⑤EF∥MN.其中正确结论的个数是( )
与EF相切;⑤EF∥MN.其中正确结论的个数是( )
A.5个
B.4个
C.3个
D.2个 -
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角板按如图所示叠放在一起,若固定
 ,将
,将 绕着公共顶点
绕着公共顶点 ,按顺时针方向旋转
,按顺时针方向旋转 度
度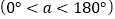 ,当
,当 的一边与
的一边与 的某一边平行时,相应的旋转角
的某一边平行时,相应的旋转角 的度数为_________________。
的度数为_________________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中,x与y的部分对应值如下表:
x
﹣3
﹣2
﹣1
0
y
0
﹣3
﹣4
﹣3
下列结论:
①ac<0;
②当x>1时,y随x的增大而增大;
③﹣4是方程ax2+(b﹣4)x+c=0的一个根;
④当﹣1<x<0时,ax2+(b﹣1)x+c+3>0.其中正确结论的个数为( )
A.4个
B.3个
C.2个
D.1个
相关试题

